Feature Engineering
이 과정에서는 훌륭한 기계 학습 모델을 구축하는 가장 중요한 단계 중 하나 인 피쳐(feature) 엔지니어링에 대해 알아 봅니다. 다음 방법을 배우게됩니다.
- 상호의존정보에서 가장 중요한 피쳐를 결정
- 여러 실제 문제 영역에서 새로운 피쳐를 개발
- target encoding을 사용하여 카디널리티가 높은 범주를 인코딩
- k-means 클러스터링으로 세분화 피쳐 생성
- 주성분 분석을 통해 데이터 세트(dataset)의 변형을 피쳐로 분해
피쳐 엔지니어링의 목표는 단순히 데이터를 문제를 해결하기에 더 적합하게 만드는 것입니다.
예를 들어 열지수 및 체감추위와 같은 “체감 온도”를 측정할 때, 우리가 직접 측정 할 수 있는 공기 온도, 습도 및 풍속을 기반으로 사람이 체감하는 온도를 측정합니다. 체감 온도는 일종의 피쳐 엔지니어링의 결과로 생각할 수 있습니다. 관측된 데이터를 우리가 알고싶은 데이터로 가공하는 것을 의미합니다.
피쳐 엔지니어링은 다음과 같은 목적으로 사용됩니다.
- 모델의 예측 성능 향상
- 계산 또는 데이터 요구 감소
- 결과의 해석 가능성 향상
피쳐 엔지니어링의 기본 원리
피쳐가 유용하려면 모델이 학습 할 수 있는 대상과의 관계가 있어야합니다. 예를 들어 선형 모델(linear model)은 선형 관계만 학습할 수 있습니다. 따라서 선형 모델을 사용할 때 목표는 대상과의 관계를 선형으로 만들기 위해 피쳐를 변환하는 것입니다.
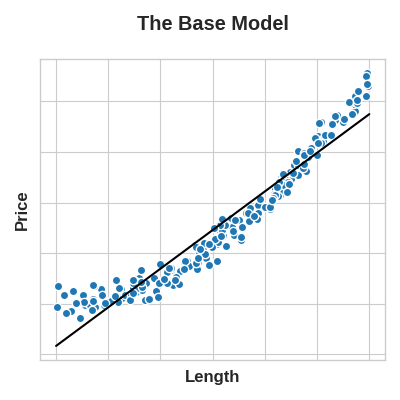
여기서 핵심 아이디어는 피쳐에 적용하는 변환(transformation)이 본질적으로 모델 자체의 일부가 된다는 것입니다. 한 면의 길이에서 토지의 정사각형 구획 가격을 예측하려한다고 가정해보십시오. 선형 모델을 길이에 직접 피팅(fitting)하면 결과가 좋지 않습니다. 관계가 선형이 아니기 때문입니다.
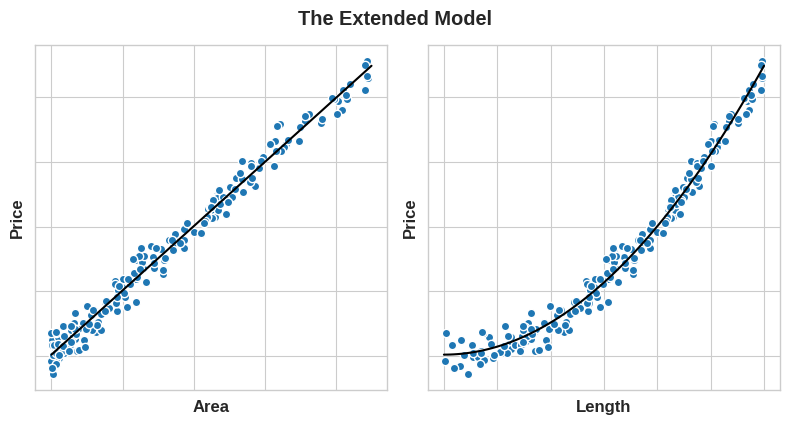
그러나 ‘Area’를 얻기 위해 Length 피쳐를 제곱하면 선형 관계가 생성됩니다. 피쳐 세트에 Area를 추가하면 이 선형 모델이 이제 포물선에 맞을 수 있습니다.
이는 피쳐 엔지니어링에 투자 된 시간에 비해 높은 성과를 내는 모습을 보여줍니다. 모델이 학습 할 수 없는 관계가 무엇이든 변환을 통해 우리가 직접 만들어 제공해 줄 수 있습니다. 피쳐 세트를 개발할 때 최상의 성능을 달성하기 위해 모델이 사용할 수 있는 정보에 대해 생각하십시오.
예제 - 콘크리트 제형
이러한 아이디어를 설명하기 위해 데이터 세트에 몇 가지 합성 피쳐를 추가하여 랜덤 포레스트 모델의 예측 성능을 향상시킬 수 있는 방법을 살펴 보겠습니다.
콘크리트 데이터 세트에는 다양한 콘크리트 제형과 결과물품의 압축 강도가 포함되어 있습니다. 이는 해당 종류의 콘크리트가 견딜 수 있는 하중의 척도입니다. 이 데이터 세트의 작업은 제형이 주어진 콘크리트의 압축 강도를 예측하는 것입니다.
1
2
3
4
5
6
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
df = pd.read_csv("input_data/concrete.csv")
df.head()
1
2
3
4
5
6
7
8
Cement BlastFurnaceSlag FlyAsh ... FineAggregate Age CompressiveStrength
0 540.0 0.0 0.0 ... 676.0 28 79.99
1 540.0 0.0 0.0 ... 676.0 28 61.89
2 332.5 142.5 0.0 ... 594.0 270 40.27
3 332.5 142.5 0.0 ... 594.0 365 41.05
4 198.6 132.4 0.0 ... 825.5 360 44.30
[5 rows x 9 columns]
여기에서 다양한 콘크리트에 들어가는 다양한 재료를 볼 수 있습니다. 우리는 이들로부터 파생 된 몇 가지 추가 합성 피쳐를 추가하는 것이, 모델이 이들 간의 중요한 관계를 학습하는 데 어떻게 도움이 되는지 잠시 후에 알게 될 것입니다.
먼저 비증강 데이터 세트에서 모델을 학습하여 기준선을 설정합니다. 이것은 우리의 새로운 피쳐가 실제로 유용한 지 판단하는 데 도움이 될 것입니다.
이와 같은 기준을 설정하는 것은 피쳐 엔지니어링 프로세스를 시작할 때 좋은 방법입니다. 기준 점수는 새 피쳐를 유지할 가치가 있는지 또는 삭제하고 다른 작업을 시도해야하는지 여부를 결정하는 데 도움이 될 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
X = df.copy()
y = X.pop("CompressiveStrength")
# Train and score baseline model
baseline = RandomForestRegressor(criterion="mae", random_state=0)
baseline_score = cross_val_score(
baseline, X, y, cv=5, scoring="neg_mean_absolute_error"
)
baseline_score = -1 * baseline_score.mean()
print(f"MAE Baseline Score: {baseline_score:.4}")
1
MAE Baseline Score: 8.232
집에서 요리 한 적이 있다면 레시피의 재료 비율이 일반적으로 절대량보다 레시피의 결과를 더 잘 예측할 수 있다는 것을 알고있을 것입니다. 그런 다음 위 기능의 비율이 CompressiveStrength의 좋은 예측 변수가 될 것이라고 추론 할 수 있습니다.
데이터 세트에 세 가지 새로운 비율 피쳐를 추가해봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
X = df.copy()
y = X.pop("CompressiveStrength")
# Create synthetic features
X["FCRatio"] = X["FineAggregate"] / X["CoarseAggregate"]
X["AggCmtRatio"] = (X["CoarseAggregate"] + X["FineAggregate"]) / X["Cement"]
X["WtrCmtRatio"] = X["Water"] / X["Cement"]
# Train and score model on dataset with additional ratio features
model = RandomForestRegressor(criterion="mae", random_state=0)
score = cross_val_score(
model, X, y, cv=5, scoring="neg_mean_absolute_error"
)
score = -1 * score.mean()
print(f"MAE Score with Ratio Features: {score:.4}")
1
MAE Score with Ratio Features: 7.948
확실히 성능이 향상되었습니다! 이는 이러한 새로운 비율 피쳐가 이전에 감지하지 못했던 모델에 중요한 정보를 노출했다는 증거입니다.
목차
- 상호의존정보(Mutual Information)
- Creating Features
- Clustering With K-Means
- 주성분분석(Principal Component Analysis)
- Target Encoding
상호의존정보(Mutual Information)
새 데이터 세트를 처음 만나는 것은 때때로 압도적이라고 느낄 수 있습니다. 설명 없이도 수백 또는 수천 개의 기능이 제공 될 수 있습니다. 어디서부터 시작해야할까요?
첫 번째 단계는 피쳐와 대상 간의 연관성을 측정하는 기능인 feature utility metric을 사용하여 순위를 구성하는 것입니다. 그런 다음 초기에 개발할 가장 유용한 피쳐의 작은 집합을 선택하고 시간을 잘 보낼 것이라는 확신을 가질 수 있습니다.
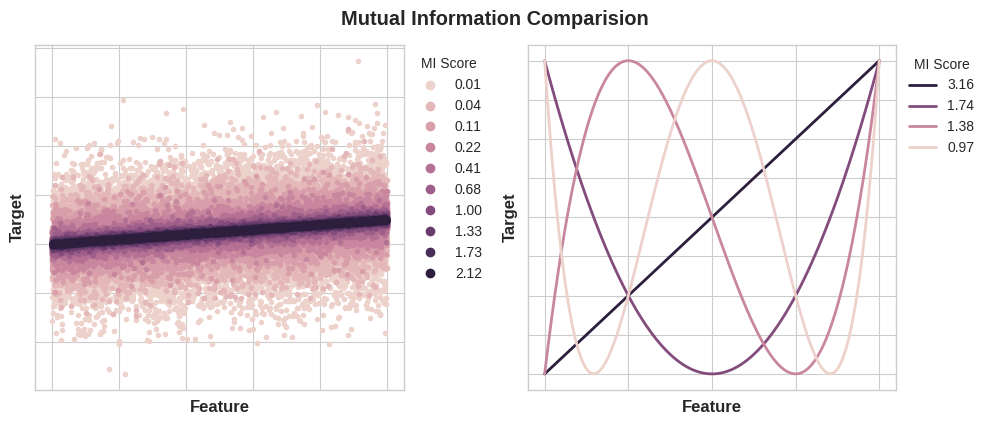
우리가 사용할 측정 항목을 “상호의존정보(MI, mutual information)”라고합니다. 상호의존정보는 두 수량 간의 관계를 측정한다는 점에서 상관 관계와 매우 유사합니다. 상호의존정보의 장점은 모든 종류의 관계를 감지 할 수 있는 반면 상관 관계는 선형 관계만 감지한다는 것입니다.
상호의존정보는 훌륭한 범용 측정 항목이며 아직 어떤 모델을 사용하고 싶은지 모를 때 기능 개발을 시작할 때 특히 유용합니다.
상호의존정보의 장점
- 사용과 해석이 쉽다.
- 계산 효율성이 좋다.
- 이론적 근거가 충분하다.
- 과적합에 강하다.
- 모든 종류의 관계를 감지할 수 있다.
상호의존정보 및 측정 대상
상호의존정보는 불확실성의 관점에서 관계를 설명합니다. 두 수량 간의 상호의존정보는 한 수량에 대한 지식이 다른 수량에 대한 불확실성을 줄이는 정도의 척도입니다. 만약 우리가 피쳐의 값을 알고 있다면 대상에 대해 얼마나 더 확신 할 수 있습니까?
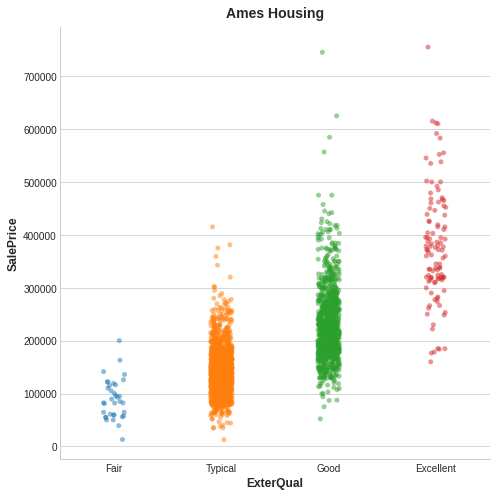
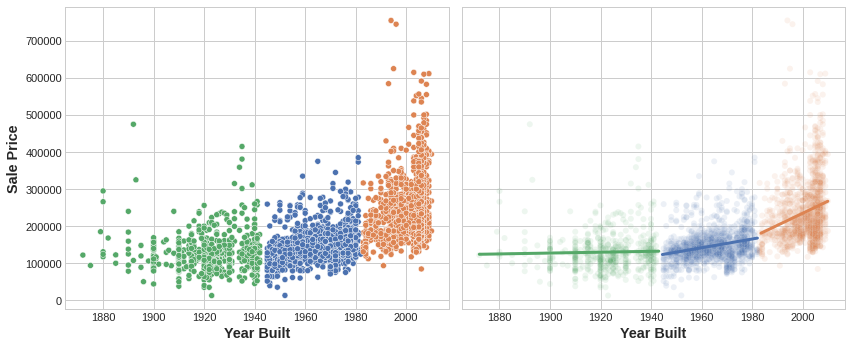
다음은 Ames Housing 데이터의 예입니다. 그림은 집의 외관 품질과 판매 가격 간의 관계를 보여줍니다. 각 점은 집을 나타냅니다.
그림에서 ExterQual의 값을 알면 해당 SalePrice에 대해 더 확실하게 알 수 있습니다. ExterQual의 각 범주는 SalePrice를 특정 범위 내로 집중시키는 경향이 있습니다. ExterQual이 SalePrice와 함께 가지고 있는 상호 정보는 ExterQual의 4가지 값을 인수한 SalePrice의 평균 불확실성 감소입니다. 예를 들어 Fair는 Typical보다 덜 자주 발생하므로 Fair는 MI 점수에서 가중치가 더 적습니다.
Technical note: What we’re calling uncertainty is measured using a quantity from information theory known as “entropy”. The entropy of a variable means roughly: “how many yes-or-no questions you would need to describe an occurance of that variable, on average.” The more questions you have to ask, the more uncertain you must be about the variable. Mutual information is how many questions you expect the feature to answer about the target.
상호의존정보 점수 해석
수량 간의 가능한 최소 상호의존정보는 0.0입니다. MI가 0일 때 서로의 관계는 완전히 독립적입니다. 반대로 이론상 MI의 상한선은 없습니다. 실제로 2.0 이상의 값은 흔하지 않습니다. (상호의존정보는 로그함수적 지표이므로 매우 느리게 증가합니다.)
다음 그림은 MI값이 피쳐와 대상과의 연관성의 종류 및 정도에 해당하는 방식에 대한 아이디어를 제공합니다.
상호의존정보를 적용 할 때 기억해야 할 사항은 다음과 같습니다.
- MI는 자체적으로 고려되는 대상의 예측 변수로서 피쳐의 상대적 잠재력을 이해하는 데 도움이 될 수 있습니다.
- 피쳐가 다른 피쳐와 상호 작용할 때 매우 유익 할 수 있지만 그다지 유익하지 않을 수도 있습니다. MI는 피쳐 간의 상호 작용을 감지 할 수 없습니다. 일변량 측정 항목입니다.
- 피쳐의 실제 유용성은 사용하는 모델에 따라 다릅니다. 특성은 대상과의 관계가 모델이 학습 할 수 있는 경우에만 유용합니다. 기능의 MI 점수가 높다고해서 모델이 해당 정보로 무엇이든 할 수 있다는 의미는 아닙니다. 연관성을 표시하려면 먼저 피쳐를 변환해야 할 수 있습니다.
예제 - 1985년도 자동차
자동차 데이터 세트는 1985년 모델 연도의 자동차 193대로 구성됩니다. 이 데이터 세트의 목표는 make, body_style, horsepower와 같은 자동차의 23가지 기능에서 자동차의 price(target)를 예측하는 것입니다. 이 예시에서는 상호의존정보로 피쳐의 순위를 매기고 데이터 시각화를 통해 결과를 조사합니다.
1
2
3
4
5
6
7
8
9
10
11
12
import matplotlib.pyplot as plt
import pandas as pd
plt.style.use("seaborn-whitegrid")
data_path = 'input_data/autos.csv'
# Replace '?' with null value
df = pd.read_csv(data_path, na_values='?')
# Exclude data with null price
df = df[df['price'].notna()]
df.head()
1
2
3
4
5
6
7
8
symboling normalized-losses make ... city-mpg highway-mpg price
0 3 NaN alfa-romero ... 21 27 13495.0
1 3 NaN alfa-romero ... 21 27 16500.0
2 1 NaN alfa-romero ... 19 26 16500.0
3 2 164.0 audi ... 24 30 13950.0
4 2 164.0 audi ... 18 22 17450.0
[5 rows x 26 columns]
MI에 대한 scikit-learn 알고리즘은 이산 피쳐를 연속 피쳐와 다르게 처리합니다. 따라서 어떤 종류의 피쳐인지 알려주어야합니다. 경험상 float dtype을 가져야하는 모든 것은 이산적이지 않습니다. 범주형(객체 또는 범주형 dtype)은 레이블 인코딩을 제공하여 이산형으로 처리 할 수 있습니다.
1
2
3
4
5
6
7
8
9
X = df.copy()
y = X.pop("price")
# Label encoding for categoricals
for colname in X.select_dtypes("object"):
X[colname], _ = X[colname].factorize()
# All discrete features should now have integer dtypes (double-check this before using MI!)
discrete_features = X.dtypes == int
데이터가 기존 튜토리얼과 다르기 때문에 추가적인 처리가 필요합니다. 결측값 대치(Imputation)를 이용해 결측값을 없애줍니다.
1
2
3
4
5
6
7
from sklearn.impute import SimpleImputer
# Imputation
my_imputer = SimpleImputer()
imputed_X = pd.DataFrame(my_imputer.fit_transform(X))
# Imputation removed column names; put them back
imputed_X.columns = X.columns
Scikit-learn에는 feature_selection 모듈에 두 개의 상호의존정보 메트릭이 있습니다. 하나는 실제값 targets(mutual_info_regression)이고 다른 하나는 범주형 targets(mutual_info_classif)입니다. 우리의 목표 가격은 실제값입니다. 아래 코드는 피쳐에 대한 MI 점수를 계산하고 이를 멋진 데이터 프레임으로 래핑합니다.
1
2
3
4
5
6
7
8
9
10
from sklearn.feature_selection import mutual_info_regression
def make_mi_scores(X, y, discrete_features):
mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
mi_scores = mi_scores.sort_values(ascending=False)
return mi_scores
mi_scores = make_mi_scores(imputed_X, y, discrete_features)
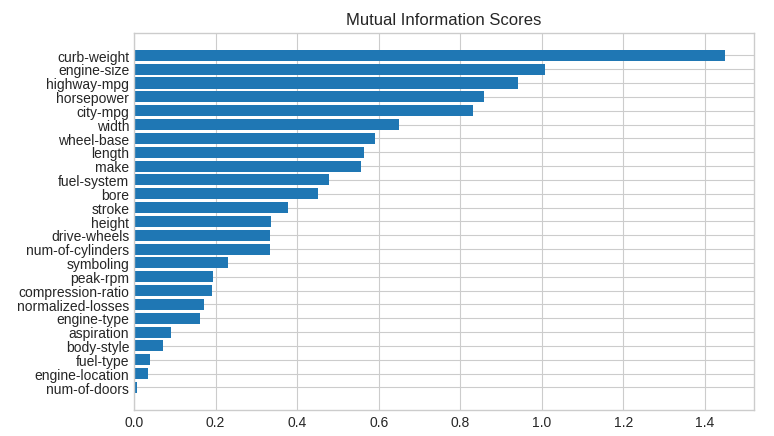
mi_scores[::3] # show a few features with their MI scores
1
2
3
4
5
6
7
8
9
10
curb-weight 1.448852
horsepower 0.858156
wheel-base 0.590054
fuel-system 0.477124
height 0.336631
symboling 0.229504
normalized-losses 0.171853
body-style 0.069742
num-of-doors 0.007341
Name: MI Scores, dtype: float64
이제 쉽게 비교해보기 위해 막대 그래프로 만들어봅시다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import matplotlib.pyplot as plt
import numpy as np
def plot_mi_scores(scores):
scores = scores.sort_values(ascending=True)
width = np.arange(len(scores))
ticks = list(scores.index)
plt.barh(width, scores)
plt.yticks(width, ticks)
plt.title("Mutual Information Scores")
plt.figure(dpi=100, figsize=(8, 5))
plot_mi_scores(mi_scores)
데이터 시각화는 유틸리티 순위에 대한 훌륭한 후속 조치입니다. 이 두 가지를 자세히 살펴 보겠습니다.
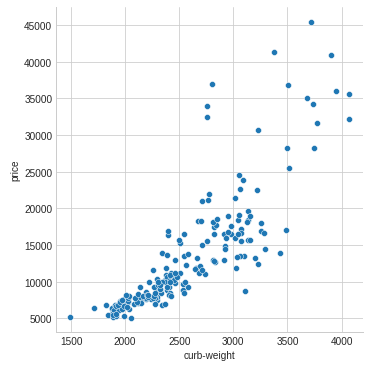
예상 할 수 있듯이 높은 점수를 받는 curb_weight 피쳐는 목표인 price와 강력한 관계를 나타냅니다.
1
2
3
import seaborn as sns
sns.relplot(x="curb-weight", y="price", data=df)
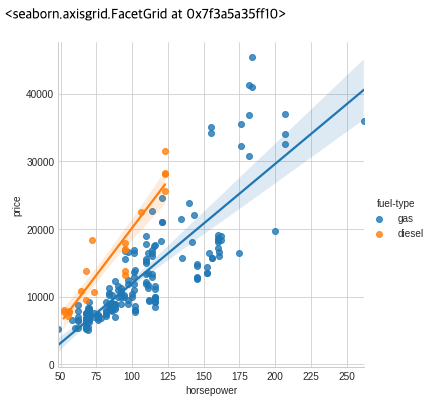
fuel_type 피쳐는 MI 점수가 상당히 낮지만 그림에서 볼 수 있듯이 horsepower 피쳐 내에서 다른 추세를 가진 두 price 인구를 명확하게 구분합니다. 이것은 fuel_type이 상호의존작용 효과에 기여하지만 결과적으론 중요하지 않을 수 있음을 나타냅니다. 피쳐를 결정하기 전에 MI 점수에서 중요하지 않은 상호의존작용 효과를 조사하는 것이 좋습니다. 도메인 지식은 여기에서 많은 지침을 제공 할 수 있습니다.
1
sns.lmplot(x="horsepower", y="price", hue="fuel-type", data=df)
데이터 시각화는 피쳐 엔지니어링 도구 상자에 추가된 훌륭한 기능입니다. 상호의존정보와 같은 유틸리티 메트릭과 함께 이와 같은 시각화는 데이터에서 중요한 관계를 발견하는 데 도움이 될 수 있습니다.
Creating Features
잠재력이 있는 피쳐 세트를 식별했으면 이제 개발을 시작할 때입니다. 여기에서는 Pandas에서 전적으로 수행 할 수 있는 몇 가지 일반적인 변환에 대해 알아봅니다.
먼저 데이터 프레임의 열 이름을 파이썬 친화적이게 바꿔주는 함수를 정의해봅니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import pandas as pd
import re
def camel_to_snake(text):
under_scorer_1 = re.compile(r'(.)([A-Z][a-z]+)')
under_scorer_2 = re.compile('([a-z0-9])([A-Z])')
subbed = under_scorer_1.sub(r'\1_\2', text)
return under_scorer_2.sub(r'\1_\2', subbed).lower()
def get_df(path, na_values=None, nrows=None):
# Get column names of DF
column_name_list = list(pd.read_csv(path, nrows=1).columns)
for c_idx in range(len(column_name_list)):
# Convert camel to snake
c_name = camel_to_snake(column_name_list[c_idx])
# remove bracket
pattern = re.compile(r'\([^)]*\)| +|-+')
c_name = pattern.sub('_', c_name)
# Remove duplicated _
pattern = re.compile(r'_+')
c_name = pattern.sub('_', c_name)
# Strip _
c_name = c_name.strip('_')
column_name_list[c_idx] = c_name
df = pd.read_csv(path, na_values=na_values, nrows=nrows)
# Change column names
df.columns = column_name_list
return df
여기에서는 미국 교통사고, 1985년대 자동차, 콘크리트 제형 및 고객 평생 가치와 같은 다양한 피쳐 유형이 있는 4개의 데이터 세트를 사용합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
plt.rc('figure', autolayout=True)
plt.rc(
'axes',
labelweight='bold',
labelsize='large',
titleweight='bold',
titlesize=14,
titlepad=10,
)
accidents = get_df('input_data/accidents.csv', nrows=20000, na_values='?')
autos = get_df('input_data/autos.csv', na_values='?')
concrete = get_df('input_data/concrete.csv', na_values='?')
customer = get_df('input_data/customer.csv', na_values='?')
새로운 피쳐 발견을 위한 팁
- 피쳐를 이해하십시오. 가능한 경우 데이터 세트의 데이터 문서를 참조하세요.
- 문제 영역을 조사하여 영역 지식을 습득하십시오. 집값을 예측하는 데 문제가 있다면 부동산에 대한 조사를 해보십시오. Wikipedia는 좋은 출발점이 될 수 있지만 책과 저널 기사는 종종 최고의 정보를 가지고 있습니다.
- 이전 작업들을 공부하십시오. 과거 Kaggle 대회의 솔루션 글은 훌륭한 리소스입니다.
- 데이터 시각화를 사용하십시오. 시각화는 단순화 할 수 있는 복잡한 관계 또는 피쳐의 분포에서 병리를 나타낼 수 있습니다. 피쳐 엔지니어링 프로세스를 진행하면서 데이터 세트를 시각화해야합니다.
수학적 변환(Mathematical Transforms)
수치적 특징 간의 관계는 종종 수학적 공식을 통해 표현되며, 도메인 연구의 일부로 자주 접하게됩니다. Pandas에서는 일반 숫자처럼 산술 연산을 열에 적용 할 수 있습니다.
Automobile 데이터 세트에는 자동차의 엔진을 설명하는 피쳐가 있습니다. 연구를 통해 잠재적으로 유용한 새 피쳐를 만들기위한 다양한 공식이 제공됩니다. 예를 들어, “stroke ratio”은 엔진의 효율성과 성능의 척도입니다.
1
2
autos["stroke_ratio"] = autos.stroke / autos.bore
autos[["stroke", "bore", "stroke_ratio"]].head()
1
2
3
4
5
6
stroke bore stroke-ratio
0 2.68 3.47 0.772334
1 2.68 3.47 0.772334
2 3.47 2.68 1.294776
3 3.40 3.19 1.065831
4 3.40 3.19 1.065831
조합이 복잡할수록 엔진의 “displacement”에 대한 공식과 같이 엔진의 힘을 측정하는 공식을 모델이 학습하기가 더 어려워집니다.
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
# Change autos.num_of_cylinders feature to int64 type
num_list = ['zero', 'one', 'two', 'three', 'four', 'five', 'six', 'seven', 'eight', 'nine', 'ten', 'eleven', 'twelve']
autos.num_of_cylinders = autos.num_of_cylinders.map(lambda noc: num_list.index(noc))
# Add displacement feature
autos["displacement"] = (
np.pi * ((0.5 * autos.bore) ** 2) * autos.stroke * autos.num_of_cylinders
)
autos[["stroke", "bore", "num_of_cylinders", "displacement"]].head()
1
2
3
4
5
6
stroke bore num_of_cylinders displacement
0 2.68 3.47 4 101.377976
1 2.68 3.47 4 101.377976
2 3.47 2.68 6 117.446531
3 3.40 3.19 4 108.695147
4 3.40 3.19 5 135.868934
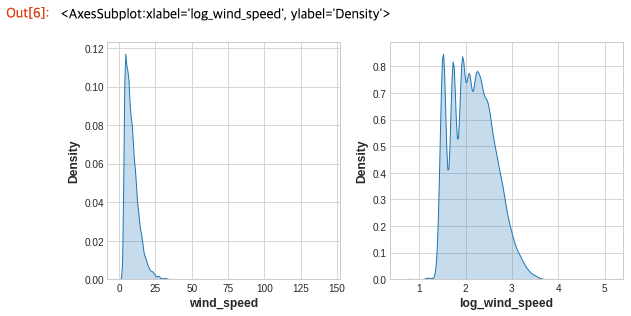
데이터 시각화는 변환, 종종 거듭 제곱 또는 로그를 통한 피쳐의 “reshaping”을 제안 할 수 있습니다. 예를 들어 미국 교통사고에서 WindSpeed의 분포는 매우 왜곡되어 있습니다. 이 경우 로그는 정규화에 효과적입니다.
1
2
3
4
5
6
7
8
9
import seaborn as sns
# If the feature has 0.0 values, use np.log1p (log(1+x)) instead of np.log
accidents['log_wind_speed'] = accidents.wind_speed.apply(np.log1p)
# Plot a comparison
fig, axs = plt.subplots(1, 2, figsize=(8, 4))
sns.kdeplot(accidents.wind_speed, shade=True, ax=axs[0])
sns.kdeplot(accidents.log_wind_speed, shade=True, ax=axs[1])
Counts
어떤 것의 존재 또는 부재를 설명하는 특징들은 종종 질병의 위험 요소들의 집합으로 나타납니다. count를 생성하여 이러한 피쳐를 집계 할 수 있습니다.
이러한 기능은 바이너리(1은 존재, 0은 부재) 또는 부울(True 또는 False)입니다. 파이썬에서 부울은 마치 정수인 것처럼 더할 수 있습니다.
교통 사고에는 도로의 지형지물이 사고 장소 근처에 있었는지 여부를 나타내는 몇 가지 피쳐가 있습니다. 이것을 이용해 sum 메소드로 사고 장소 근처의 도로 지형지물의 총 개수를 나타낼 수 있습니다.
1
2
3
4
5
6
7
8
roadway_features = [
"amenity", "bump", "crossing", "give_way", "junction",
"no_exit", "railway", "roundabout", "station", "stop",
"traffic_calming", "traffic_signal"
]
accidents["roadway_features"] = accidents[roadway_features].sum(axis=1)
accidents[roadway_features + ["roadway_features"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
12
13
amenity bump crossing ... traffic_calming traffic_signal roadway_features
0 False False False ... False False 0
1 False False False ... False False 0
2 False False False ... False True 1
3 False False False ... False False 0
4 False False False ... False True 1
5 False False False ... False False 0
6 False False False ... False False 0
7 False False False ... False False 0
8 False False False ... False False 0
9 False False False ... False False 0
[10 rows x 13 columns]
데이터 프레임의 기본 제공 메서드를 사용하여 부울값을 만들 수도 있습니다. 콘크리트 데이터 세트에는 콘크리트 제형에 포함된 성분의 양이 있습니다. 많은 공식에는 하나 이상의 구성 요소가 포함되지않습니다(즉, 구성 요소의 값이 0 임). 아래 코드는 데이터 프레임에 내장된 gt 메소드를 사용하여 공식에 포함된 구성 요소의 수를 계산합니다.
1
2
3
4
5
6
components = [
"cement", "blast_furnace_slag", "fly_ash", "water", "superplasticizer",
"coarse_aggregate", "fine_aggregate"
]
concrete["components"] = concrete[components].gt(0).sum(axis=1)
concrete[components + ["components"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
12
13
cement blast_furnace_slag ... fine_aggregate components
0 540.0 0.0 ... 676.0 5
1 540.0 0.0 ... 676.0 5
2 332.5 142.5 ... 594.0 5
3 332.5 142.5 ... 594.0 5
4 198.6 132.4 ... 825.5 5
5 266.0 114.0 ... 670.0 5
6 380.0 95.0 ... 594.0 5
7 380.0 95.0 ... 594.0 5
8 266.0 114.0 ... 670.0 5
9 475.0 0.0 ... 594.0 4
[10 rows x 8 columns]
Building-Up and Breaking-Down Features
종종 다음과 같이 더 간단한 조각으로 나눌 수있는 복잡한 문자열이 있습니다.
- ID numbers: ‘123-45-6789’
- Phone numbers: ‘(999) 555-0123’
- Street addresses: ‘8241 Kaggle Ln., Goose City, NV’
- Internet addresses: ‘http://www.kaggle.com’
- Product codes: ‘0 36000 29145 2’
- Dates and times: ‘Mon Sep 30 07:06:05 2013’
이와 같은 피쳐에는 종종 사용할 수 있는 일종의 구조가 있습니다. 예를 들어 미국 전화 번호에는 발신자의 위치를 알려주는 지역 번호(‘(999)’부분)가 있습니다. 항상 그렇듯이 일부 연구는 여기에서 성과를 거둘 수 있습니다.
str 접근자를 사용하면 split과 같은 문자열 메서드를 열에 직접 적용 할 수 있습니다. 고객 평생 가치 데이터 세트에는 보험 회사의 고객을 설명하는 피쳐가 포함되어 있습니다. Policy 피쳐에서, 우리는 Level과 Type을 분리 할 수 있습니다.
1
2
3
4
customer[["type", "level"]] = (
customer["policy"].str.split(" ", expand=True)
)
customer[["policy", "type", "level"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
policy type level
0 Corporate L3 Corporate L3
1 Personal L3 Personal L3
2 Personal L3 Personal L3
3 Corporate L2 Corporate L2
4 Personal L1 Personal L1
5 Personal L3 Personal L3
6 Corporate L3 Corporate L3
7 Corporate L3 Corporate L3
8 Corporate L3 Corporate L3
9 Special L2 Special L2
조합에 상호 작용이 있다고 믿을만한 이유가 있다면 피쳐를 결합 할 수도 있습니다.
1
2
autos["make_and_style"] = autos["make"] + "_" + autos["body_style"]
autos[["make", "body_style", "make_and_style"]].head()
1
2
3
4
5
6
make body_style make_and_style
0 alfa-romero convertible alfa-romero_convertible
1 alfa-romero convertible alfa-romero_convertible
2 alfa-romero hatchback alfa-romero_hatchback
3 audi sedan audi_sedan
4 audi sedan audi_sedan
Group Transforms
마지막으로 일부 범주별로 그룹화 된 여러 행에 걸쳐 정보를 집계하는 그룹 변환(Group Transforms)이 있습니다. 그룹 변환을 사용하여 “사람의 거주 국가 평균 수입” 또는 “장르별 평일에 개봉 된 영화의 비율”과 같은 피쳐를 만들 수 있습니다. 범주 상호 작용을 발견 한 경우 해당 범주에 대한 그룹 변환을 조사하는 것이 좋습니다.
집계 함수를 사용하여 그룹 변환은 그룹화를 제공하는 범주형 피쳐와 값을 집계하려는 다른 피쳐의 두 피쳐를 결합합니다. “주별 평균 소득”의 경우 그룹화 기능에 대해 State를 선택하고 집계 함수에 대해 mean을 선택하고 집계 피쳐에 대해 Income을 선택합니다. Pandas에서 이를 계산하기 위해 groupby 및 transform 메서드를 사용합니다.
1
2
3
4
customer["average_income"] = (
customer.groupby("state")["income"].transform("mean")
)
customer[["state", "income", "average_income"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
state income average_income
0 Washington 56274 38122.733083
1 Arizona 0 37405.402231
2 Nevada 48767 38369.605442
3 California 0 37558.946667
4 Washington 43836 38122.733083
5 Oregon 62902 37557.283353
6 Oregon 55350 37557.283353
7 Arizona 0 37405.402231
8 Oregon 14072 37557.283353
9 Oregon 28812 37557.283353
mean 함수는 기본 제공 데이터 프레임 메서드이므로 변환할 문자열로 전달할 수 있습니다. 다른 편리한 방법으로는 max, min, median, var, std 및 count가 있습니다. 데이터 세트에서 각 상태가 발생하는 빈도를 계산하는 방법은 다음과 같습니다.
1
2
3
4
customer["state_freq"] = (
customer.groupby("state")["state"].transform("count") / customer.state.count()
)
customer[["state", "state_freq"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
state state_freq
0 Washington 0.087366
1 Arizona 0.186446
2 Nevada 0.096562
3 California 0.344865
4 Washington 0.087366
5 Oregon 0.284760
6 Oregon 0.284760
7 Arizona 0.186446
8 Oregon 0.284760
9 Oregon 0.284760
이와 같은 변환을 사용하여 범주형 피쳐에 대한 “frequency encoding”을 만들 수 있습니다.
훈련 및 검증 분할을 사용하는 경우 독립성을 유지하려면 훈련 세트만 사용하여 그룹화 된 기능을 생성한 다음 검증 세트에 조인하는 것이 가장 좋습니다. 훈련 세트에서 drop_duplicates를 사용하여 고유한 값 세트를 생성한 후 검증 세트의 merge 메서드를 사용할 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Create splits
df_train = customer.sample(frac=0.5)
df_valid = customer.drop(df_train.index)
# Create the average claim amount by coverage type, on the training set
df_train["average_claim"] = df_train.groupby("coverage")["total_claim_amount"].transform("mean")
# Merge the values into the validation set
df_valid = df_valid.merge(
df_train[["coverage", "average_claim"]].drop_duplicates(),
on="coverage",
how="left",
)
df_valid[["coverage", "average_claim"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
coverage average_claim
0 Premium 643.230579
1 Basic 376.021438
2 Premium 643.230579
3 Extended 481.159342
4 Basic 376.021438
5 Basic 376.021438
6 Basic 376.021438
7 Basic 376.021438
8 Basic 376.021438
9 Premium 643.230579
Tips on Creating Features
피쳐를 만들 때 모델의 강점과 약점을 염두에 두는 것이 좋습니다. 다음은 몇 가지 지침입니다.
- 선형 모델은 합과 차이를 자연스럽게 학습하지만 더 복잡한 것은 학습 할 수 없습니다.
- 비율(Ratios)은 대부분의 모델이 배우기 어려운 것 같습니다. 비율 조합은 종종 몇 가지 쉬운 성능 향상으로 이어집니다.
- 선형 모델과 신경망은 일반적으로 정규화 된 기능에서 더 잘 수행됩니다. 신경망은 특히 0에서 너무 멀지 않은 값으로 개선된 피쳐가 필요합니다. 트리 기반 모델(예: 랜덤 포레스트 및 XGBoost)은 때때로 정규화의 이점을 얻을 수 있지만 일반적으론 거의 그렇지 못 합니다.
- 트리 모델은 거의 모든 피쳐 조합을 근사화하는 방법을 배울 수 있지만 조합이 특히 중요한 경우, 특히 데이터가 제한된 경우 명시적으로 생성하면 이점을 얻을 수 있습니다.
- 개수(Counts)는 트리 모델에 특히 유용합니다. 이러한 모델에는 한 번에 여러 피쳐에 걸쳐 정보를 집계하는 자연스러운 방법이 없기 때문입니다.
Clustering With K-Means
이제부터 비지도 학습 알고리즘을 활용해봅시다. 비지도 알고리즘은 대상을 사용하지 않습니다. 대신, 그들의 목적은 특정 방식으로 피쳐의 구조를 나타내기 위해 데이터의 일부 속성을 학습하는 것입니다. 예측을 위한 피쳐 엔지니어링의 맥락에서 비지도 알고리즘은 “피쳐 발견” 기술이라 할 수 있습니다.
클러스터링(Clustering)은 단순히 포인트가 서로 얼마나 유사한 지에 따라 그룹에 데이터 포인트를 할당하는 것을 의미합니다. 클러스터링 알고리즘은 말하자면 “유유상종”입니다.
피쳐 엔지니어링에 사용되는 경우, 예를 들어 우리는 시장 부문을 대표하는 고객 그룹 또는 유사한 날씨 패턴을 공유하는 지리적 영역을 발견 할 수 있습니다. 클러스터 레이블 피쳐를 추가하면 기계 학습 모델이 공간 또는 근접성의 복잡한 관계를 풀 수 있습니다.
Cluster Labels as a Feature
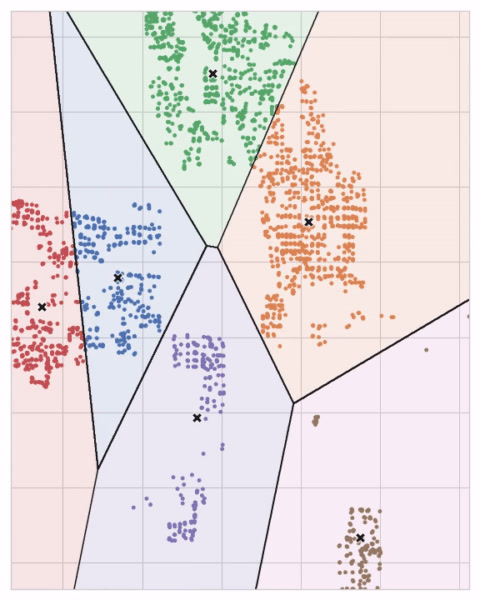
단일 real-valued 피쳐에 적용되는 클러스터링은 기존의 “비닝(binning)”또는 “이산화(discretization)“변환처럼 작동합니다. 여러 피쳐에서 이는 “다차원 비닝”(벡터 양자화라고도 함)과 같습니다.
 Left: Clustering a single feature. Right: Clustering across two features.
Left: Clustering a single feature. Right: Clustering across two features.
데이터 프레임에 추가 된 클러스터 레이블의 피쳐는 다음과 같습니다.
1
2
3
4
5
Longitude Latitude Cluster
-93.619 42.054 3
-93.619 42.053 3
-93.638 42.060 1
-93.602 41.988 0
이 클러스터 피쳐는 범주형이라는 것을 기억하는 것이 중요합니다. 여기에서는 일반적인 클러스터링 알고리즘이 생성하는 레이블 인코딩(즉, 정수 시퀀스)으로 표시됩니다. 모델에 따라 원-핫 인코딩이 더 적절할 수 있습니다.
클러스터 레이블 추가에 대한 동기 부여 아이디어는 클러스터가 피쳐 간의 복잡한 관계를 더 간단한 청크(chunk)로 분할한다는 것입니다. 그런 다음 우리 모델은 복잡한 전체를 한 번에 배워야하는 대신 더 간단한 청크를 하나씩 학습 할 수 있습니다. 이것이 “분할 및 정복(divide and conquer)” 전략입니다.
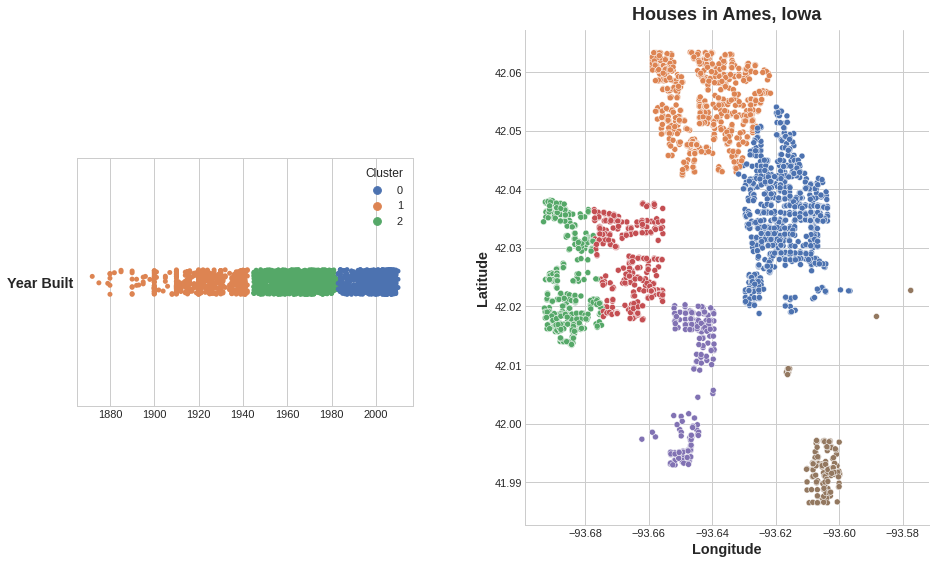
그림은 클러스터링이 어떻게 단순 선형 모델을 개선 할 수 있는지 보여줍니다. YearBuilt와 SalePrice 간의 곡선 관계는 이러한 종류의 모델에 비해 너무 복잡합니다. 그러나 더 작은 청크에서는 관계가 거의 선형 적이며 모델이 더 쉽게 학습 할 수 있습니다.
k-Means Clustering
많은 클러스터링 알고리즘이 있습니다. 이들은 주로 “유사성(similarity)” 또는 “근접성(proximity)”을 측정하는 방법과 함께 작동하는 피쳐의 종류가 다릅니다. 우리가 사용할 알고리즘인 k-평균(k-means)은 직관적이고 피쳐 엔지니어링 컨텍스트에 적용하기 쉽습니다. 응용 프로그램에 따라 다른 알고리즘이 더 적합 할 수 있습니다.
k-평균 군집화(k-means clustering)는 일반적인 직선 거리(즉, 유클리드 거리)를 사용하여 유사성을 측정합니다. 피쳐 공간 내부에 중심점(centroids)이라고하는 여러 점을 배치하여 클러스터를 생성합니다. 데이터 세트의 각 점은 가장 가까운 중심의 클러스터에 할당됩니다. “k-means”의 “k”는 생성하는 중심(즉, 클러스터) 수입니다. k는 직접 정의합니다.
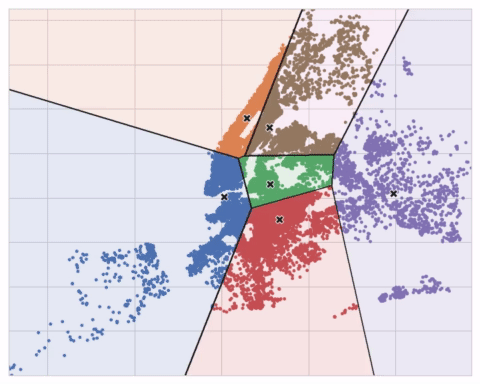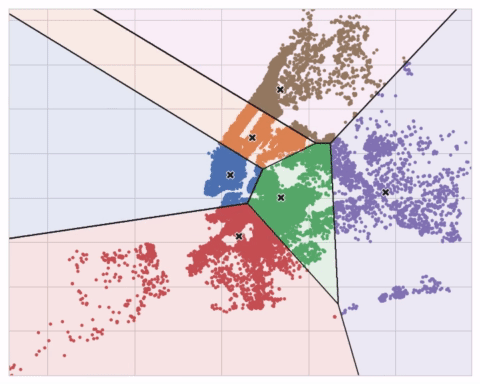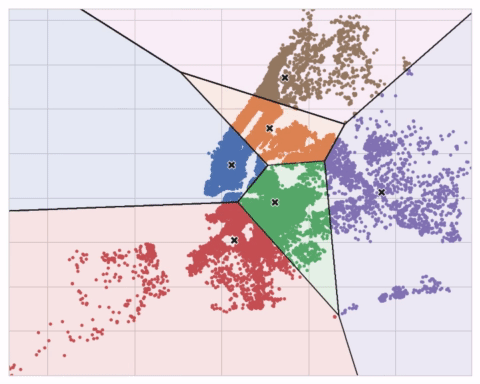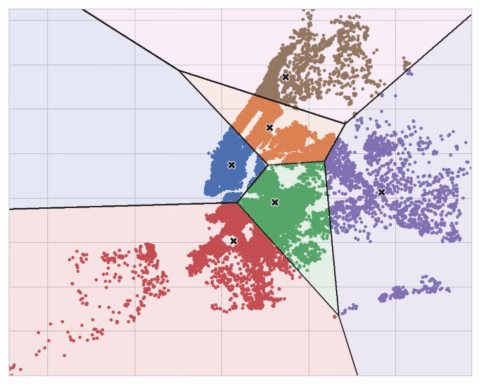
맞닿은 중심점의 원 세트가 겹치면 선을 형성합니다. 그 결과 보로노이 테살레이션(Voronoi tessellation)이라고합니다. 테살레이션은 향후 데이터가 할당 될 클러스터를 보여줍니다. 테살레이션은 본질적으로 k-평균이 훈련 데이터에서 학습하는 것입니다.
위의 Ames 데이터 세트에 대한 클러스터링은 k-평균 클러스터링입니다. 다음은 테살레이션과 중심점이 표시된 그림입니다.
k-평균 알고리즘이 클러스터를 학습하는 방법과 이것이 피쳐 엔지니어링에 대해 의미하는 바를 검토해 보겠습니다. 우리는 scikit-learn 구현의 세 가지 매개 변수인 n_clusters, max_iter, n_init에 초점을 맞출 것입니다.
이것은 간단한 2단계 과정을 가집니다. 알고리즘은 사전 정의 된 수(n_clusters)의 중심점을 무작위로 초기화하는 것으로 시작합니다. 그런 다음, 다음 두 작업을 반복합니다.
- 가장 가까운 군집 중심점에 점 할당
- 각 중심점을 이동시켜 점까지의 거리를 최소화합니다.
중심점이 더 이상 움직이지 않거나 최대 반복 횟수(max_iter)에 다다를 때까지 이 두 단계를 반복합니다.
중심점의 초기 임의 위치가 불량한 클러스터링으로 끝나는 경우가 종종 있습니다. 이러한 이유로 알고리즘은 여러 번(n_init)을 반복하고 각 점과 중심점 사이의 총 거리가 가장 적은 클러스터링, 최적 클러스터링을 반환합니다.
아래 애니메이션은 작동중인 알고리즘을 보여줍니다. 초기 중심점에 대한 결과의 의존성과 수렴까지 반복하는 것의 중요성을 보여줍니다.
많은 클러스터의 경우 max_iter를, 복잡한 데이터 세트의 경우 n_init를 늘려야 할 수 있습니다. 일반적으로 직접 선택해야하는 유일한 매개 변수는 n_clusters(즉, k)입니다. 피쳐 집합에 대한 최상의 분할은 사용중인 모델과 예측하려는 항목에 따라 다르므로 모든 하이퍼 파라미터처럼 조정하는 것이 가장 좋습니다(예 : 교차 유효성 검사(cross-validation)를 통해).
Example - California Housing
공간적 피쳐로서 California Housing의 ‘위도’ 및 ‘경도’는 k-평균 클러스터링에 대한 자연스러운 후보를 만듭니다. 이 예에서는 이를 ‘median_income’(중위 소득)과 클러스터링하여 캘리포니아의 여러 지역에서 경제 세그먼트를 생성합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
df = pd.read_csv("input_data/housing.csv")
X = df.loc[:, ["median_income", "latitude", "longitude"]]
X.head()
1
2
3
4
5
6
median_income latitude longitude
0 8.3252 37.88 -122.23
1 8.3014 37.86 -122.22
2 7.2574 37.85 -122.24
3 5.6431 37.85 -122.25
4 3.8462 37.85 -122.25
k- 평균 클러스터링은 스케일에 민감하므로 극단적인 값으로 데이터를 다시 스케일링하거나 정규화하는 것이 좋습니다. 우리의 피쳐는 이미 거의 같은 규모이므로 그대로 두겠습니다.
1
2
3
4
5
6
# Create cluster feature
kmeans = KMeans(n_clusters=6)
X["cluster"] = kmeans.fit_predict(X)
X["cluster"] = X["cluster"].astype("category")
X.head()
1
2
3
4
5
6
median_income latitude longitude cluster
0 8.3252 37.88 -122.23 2
1 8.3014 37.86 -122.22 2
2 7.2574 37.85 -122.24 2
3 5.6431 37.85 -122.25 2
4 3.8462 37.85 -122.25 1
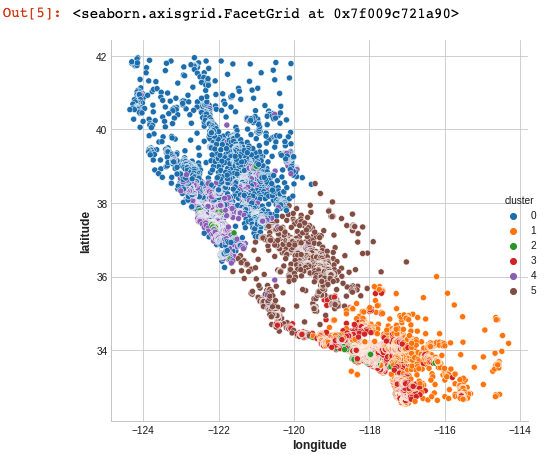
이제 이것이 얼마나 효과적인지 알아보기 위해 몇 가지 플롯을 살펴 보겠습니다. 첫째, 군집의 지리적 분포를 보여주는 산점도입니다. 알고리즘이 해안의 고소득 지역에 대해 별도의 세그먼트를 만든 것 같습니다.
1
sns.relplot(x="longitude", y="latitude", hue="cluster", data=X, height=6)
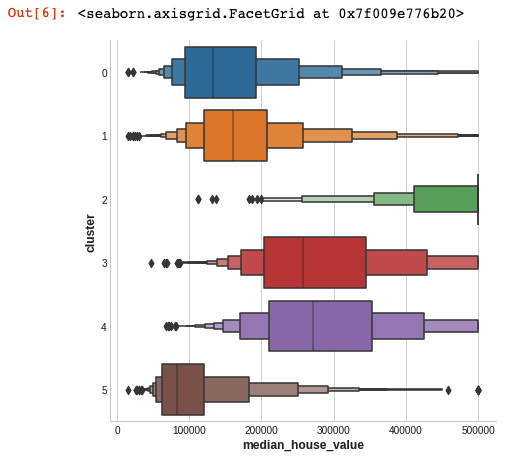
이 데이터 세트의 대상은 median_house_value( 평균 주택 가치)입니다. 이 box-plots은 각 군집 내의 대상 분포를 보여줍니다. 클러스터링이 정보를 제공하는 경우 이러한 분포는 대부분 median_house_value에서 분리되어야합니다.
주성분분석(Principal Component Analysis)
클러스터링이 근접성을 기반으로 데이터 세트를 분할하는 것처럼 PCA를 데이터 변동의 분할로 생각할 수 있습니다. PCA는 데이터에서 중요한 관계를 발견하는 데 도움이되는 훌륭한 도구이며 더 많은 정보를 제공하는 기능을 만드는 데 사용할 수도 있습니다.
Technical note: PCA는 일반적으로 표준화 된 데이터에 적용됩니다. 표준화 된 데이터를 사용하는 경우 “변동(variation)”은 “상관 관계(correlation)”를 의미합니다. 표준화되지 않은 데이터를 사용하는 경우 “변동”은 “공분산(covariance)”을 의미합니다.이 과정의 모든 데이터는 PCA를 적용하기 전에 표준화됩니다.
Abalone 데이터 세트에는 수천 개의 Tasmanian 전복에서 가져온 물리적 측정이 있습니다. 지금은 몇 가지 피쳐인 조개 껍질의 ‘Height(높이)’와 ‘Diameter(직경)’을 살펴 보겠습니다.
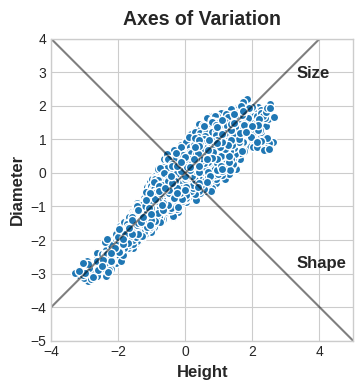
이 데이터에는 전복이 서로 다른 경향을 나타내는 “변이 축(axes of variation)”이 있다고 생각할 수 있습니다. 그림에서 이러한 축은 데이터의 자연적인 치수를 따라 이어지는 수직선으로 나타나며, 각 원래 피쳐에 대해 하나의 축이 있습니다.
종종 이러한 변형 축에 이름을 지정할 수 있습니다. 더 긴 축은 “Size(크기)” 구성 요소(component)라고 할 수 있습니다. 작은 height와 작은 diameter(왼쪽 아래)는 큰 height와 큰 diameter(오른쪽 위)과 대조됩니다. 짧은 축은 “Shape(모양)” 구성 요소라고 할 수 있습니다. 작은 height와 큰 diameter(평평한 모양)이 큰 height와 작은 diameter(둥근 모양)과 대조됩니다.
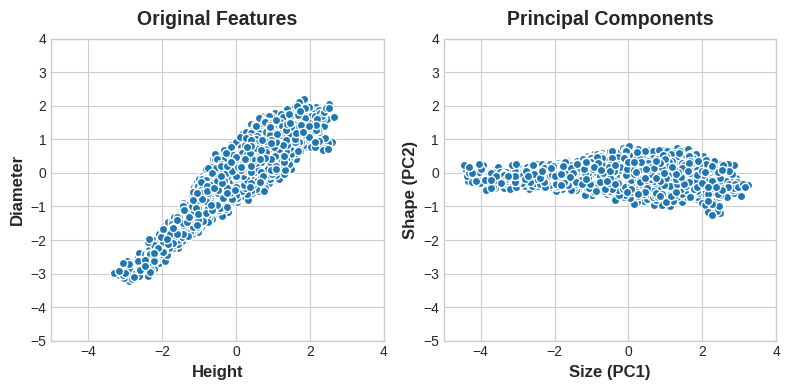
전복을 ‘Height’와 ‘Diameter’으로 설명하는 대신 ‘Size’와 ‘Shape’로 설명 할 수 있습니다. 사실 이것은 PCA의 전체 개념입니다. 원래 기능으로 데이터를 설명하는 대신 변형 축으로 데이터를 설명합니다. 변형의 축이 새로운 피쳐가 됩니다.
새로운 피쳐 PCA 구조는 실제로 원래 피쳐의 선형 조합(가중 합계)입니다.
1
2
df["Size"] = 0.707 * X["Height"] + 0.707 * X["Diameter"]
df["Shape"] = 0.707 * X["Height"] - 0.707 * X["Diameter"]
이러한 새로운 피쳐를 데이터의 주성분(principal components)이라고합니다. 가중치 자체를 로딩(loadings)이라고합니다. 원래 데이터 세트의 피쳐만큼 많은 주성분이 있을 것입니다. 2개가 아닌 10개의 피쳐를 사용했다면 10개의 성분으로 끝났을 것입니다.
성분의 로딩은 기호와 크기를 통해 표현되는 변화를 알려줍니다.
1
2
3
Features/Components Size(PC1) Shape (PC2)
Height 0.707 0.707
Diameter 0.707 -0.707
이 로딩 표는 Size 성분에서 Height와 Diameter이 같은 방향(동일 기호)이지만 Shape 성분에서는 반대 방향(반대 기호)입니다. 각 성분에서 로딩은 모두 동일한 크기이므로 피쳐가 둘 다에 동일하게 기여합니다.
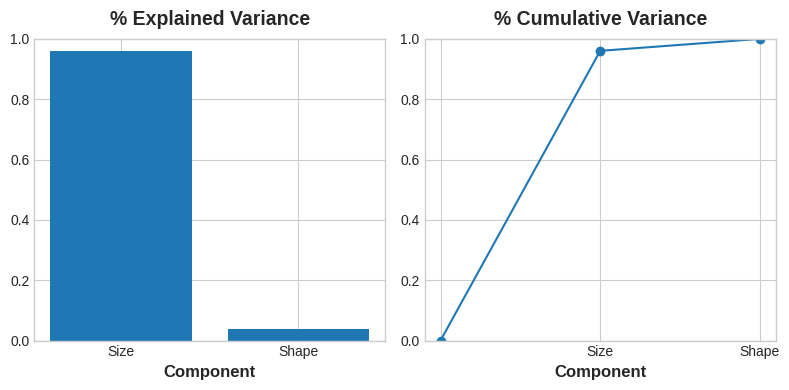
PCA는 또한 각 성분의 변동량(amount of variation)을 알려줍니다. 그림에서 Shape 성분보다 Size 성분을 따라 데이터에 더 많은 변동이 있음을 알 수 있습니다. PCA는 각 성분의 % explained variance를 통해 이를 정확하게 만듭니다.
(크기는 높이와 지름 간의 차이의 약 96%를 차지하고 모양은 약 4%를 차지합니다.)
Size 성분은 Height와 Diameter 사이의 대부분의 변화를 포착합니다. 그러나 성분의 분산 양이 예측 변수로서의 성능과 반드시 일치하는 것은 아닙니다. 예측하려는 내용에 따라 다릅니다.
PCA for Feature Engineering
피쳐 엔지니어링을 위해 PCA를 사용할 수 있는 두 가지 방법이 있습니다.
첫 번째 방법은 기술적 기술(descriptive technique)로 사용하는 것입니다. 성분이 변동에 대해 알려주기 때문에 성분에 대한 MI 점수를 계산하고 어떤 종류의 변동이 목표를 가장 잘 예측하는지 확인할 수 있습니다. 이를 통해 생성 할 피쳐의 종류에 대한 아이디어를 얻을 수 있습니다. 예를 들어 ‘Size’가 중요한 경우 ‘Height’와 ‘Diameter’의 곱, Shape가 중요한 경우 ‘Height’와 ‘Diameter’의 비율입니다. 점수가 높은 성분 중 하나 이상에서 클러스터링을 시도 할 수도 있습니다.
두 번째 방법은 성분 자체를 피쳐로 사용하는 것입니다. 성분은 데이터의 변형 구조를 직접 노출하기 때문에 원래 피쳐보다 더 많은 정보를 제공 할 수 있습니다. 다음은 몇 가지 사용 사례입니다.
- 차원 감소(Dimensionality reduction): 피쳐가 중복성이 높은 경우(특히 다중 공선) PCA는 중복성을 하나 이상의 0에 가까운 분산(near-zero variance) 성분으로 분할합니다. 그러면 정보가 거의 또는 전혀 포함되지 않으므로 삭제할 수 있습니다.
- 이상 감지(Anomaly detection): 원래 피쳐에서 분명하지 않은 비정상적인 변동은 종종 낮은 분산(low-variance) 성분에 나타납니다. 이러한 성분은 이상 또는 이상값 탐지 작업에서 매우 유익 할 수 있습니다.
- 노이즈 감소(Noise reduction): 센서 판독 값 모음은 종종 일반적인 배경 노이즈를 공유합니다. PCA는 때때로 (유익한) 신호를 더 적은 수의 피쳐로 수집하고 노이즈는 그대로 두어 signal-to-noise 비율을 높일 수 있습니다.
- 역상관(Decorrelation) : 일부 ML 알고리즘은 상관 관계가 높은 피쳐로 어려움을 겪습니다. PCA는 상관 관계가있는 피쳐를 상관 관계가 없는 성분으로 변환하므로 알고리즘이 더 쉽게 작동 할 수 있습니다.
PCA는 기본적으로 데이터의 상관 구조에 대한 직접 액세스를 제공합니다.
PCA Best Practices PCA를 적용 할 때 유의해야 할 몇 가지 사항이 있습니다.
- PCA는 연속 수량 또는 개수와 같은 숫자 피쳐에서만 작동합니다.
- PCA는 규모에 민감합니다. 타당한 이유가 없는 한 PCA를 적용하기 전에 데이터를 표준화하는 것이 좋습니다.
- 결과에 과도한 영향을 미칠 수 있으므로 이상값을 제거하거나 제한하는 것을 고려하십시오.
Example - 1985 Automobiles
이 예시에서는 Automobile 데이터 세트에서 피쳐를 발견하기 위한 기술적 기술(descriptive technique)을 사용하여 PCA를 적용합니다. 실습에서 다른 사용 사례를 살펴 보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import display
from sklearn.feature_selection import mutual_info_regression
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
def plot_variance(pca, width=8, dpi=100):
# Create figure
fig, axs = plt.subplots(1, 2)
n = pca.n_components_
grid = np.arange(1, n + 1)
# Explained variance
evr = pca.explained_variance_ratio_
axs[0].bar(grid, evr)
axs[0].set(
xlabel="component", title="% Explained Variance", ylim=(0.0, 1.0)
)
# Cumulative Variance
cv = np.cumsum(evr)
axs[1].plot(np.r_[0, grid], np.r_[0, cv], "o-")
axs[1].set(
xlabel="component", title="% Cumulative Variance", ylim=(0.0, 1.0)
)
# Set up figure
fig.set(figwidth=8, dpi=100)
return axs
def make_mi_scores(X, y, discrete_features):
mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
mi_scores = mi_scores.sort_values(ascending=False)
return mi_scores
df = pd.read_csv("input_data/autos.csv", na_values='?')
다양한 속성을 포괄하는 4가지 피쳐를 선택했습니다. 4가지의 각 피쳐는 price에 대한 높은 MI 점수를 가지고있습니다. 이러한 피쳐들은 당연히 동일한 규모가 아니기 때문에 데이터를 표준화 할 필요가 있습니다.
1
2
3
4
5
6
7
8
9
10
features = ["highway-mpg", "engine-size", "horsepower", "curb-weight"]
X = df.copy()
# Drop row with null data
X = X.dropna(subset=features+['price'])
y = X.pop('price')
X = X.loc[:, features]
# Standardize
X_scaled = (X - X.mean(axis=0)) / X.std(axis=0)
이제 우리는 scikit-learn의 PCA 추정기를 맞추고 주성분을 만들 수 있습니다. 여기에서 변환된 데이터 세트의 처음 몇 행을 볼 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
from sklearn.decomposition import PCA
# Create principal components
pca = PCA()
X_pca = pca.fit_transform(X_scaled)
# Convert to dataframe
component_names = [f"PC{i+1}" for i in range(X_pca.shape[1])]
X_pca = pd.DataFrame(X_pca, columns=component_names)
X_pca.head()
1
2
3
4
5
6
PC1 PC2 PC3 PC4
0 0.394715 -0.373767 0.071735 0.188581
1 0.394715 -0.373767 0.071735 0.188581
2 1.575528 -0.162638 0.584698 -0.244818
3 -0.397286 -0.420214 0.188498 0.033906
4 1.145809 -0.736098 -0.311617 0.254685
피팅 후 PCA 인스턴스는 components_ 속성에 로딩을 포함합니다. (아쉽게도 PCA의 용어는 일관성이 없습니다. X_pca의 변환 된 열을 components라고 부르는 규칙을 따르고 있습니다. 그렇지 않으면 이름이 없습니다.) 데이터 프레임에 로드를 래핑합니다.
1
2
3
4
5
6
loadings = pd.DataFrame(
pca.components_.T, # transpose the matrix of loadings
columns=component_names, # so the columns are the principal components
index=X.columns, # and the rows are the original features
)
loadings
1
2
3
4
5
PC1 PC2 PC3 PC4
highway-mpg -0.487876 0.742190 0.173483 -0.425481
engine-size 0.499975 0.636174 0.103199 0.578496
horsepower 0.504585 -0.099568 0.726225 -0.456154
curb-weight 0.507342 0.185804 -0.657153 -0.525577
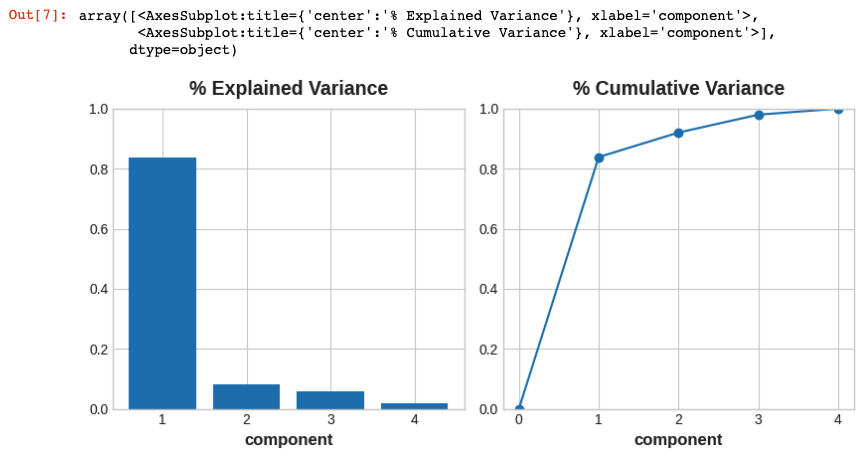
성분 부하의 부호와 크기는 캡처 된 변동의 종류를 알려줍니다. 첫 번째 성분(PC1)은 연비가 좋지 않은 크고 강력한 차량과 연비가 좋은 더 작고 경제적인 차량 간의 대조를 보여줍니다. 이것을 “Luxury/Economy” 축이라고 부를 수 있습니다. 다음 그림은 우리가 선택한 네 가지 피쳐가 대부분 Luxury/Economy 축을 따라 다양하다는 것을 보여줍니다.
성분의 MI 점수도 살펴보겠습니다. 당연히 PC1은 매우 유익하지만 나머지 성분은 작은 차이에도 불구하고 여전히 price와 상당한 관계가 있습니다. 이러한 성분을 조사하는 것은 주요 Luxury/Economy 축에서 포착되지 않은 관계를 찾는 데 유용 할 수 있습니다.
1
2
mi_scores = make_mi_scores(X_pca, y, discrete_features=False)
mi_scores
1
2
3
4
5
PC1 0.990770
PC2 0.350752
PC3 0.221004
PC4 0.134155
Name: MI Scores, dtype: float64
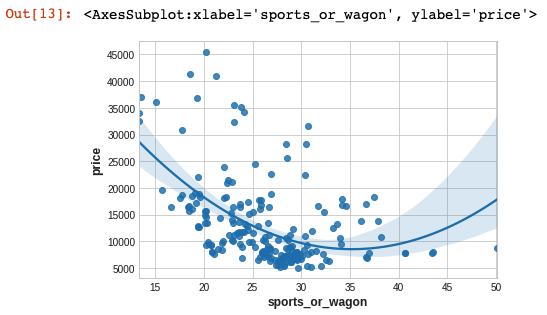
세 번째 성분은 horsepower와 curb-weight – sports cars vs wagons의 대조를 보여줍니다.
1
2
3
4
# Show dataframe sorted by PC3
idx = X_pca["PC3"].sort_values(ascending=False).index
cols = ["make", "body-style", "horsepower", "curb-weight"]
df.loc[idx, cols]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
make body-style horsepower curb-weight
123 plymouth wagon 88.0 2535
124 plymouth hatchback 145.0 2818
125 porsche hatchback 143.0 2778
46 isuzu hatchback 90.0 2734
102 nissan wagon 152.0 3296
.. ... ... ... ...
106 nissan hatchback 160.0 3139
110 peugot wagon 95.0 3430
107 peugot sedan 97.0 3020
111 peugot sedan 95.0 3075
149 subaru wagon 111.0 2650
[199 rows x 4 columns]
이 대비를 표현하기 위해 새로운 비율 피쳐를 만들어 보겠습니다.
1
2
df["sports_or_wagon"] = X['curb-weight'] / X.horsepower
sns.regplot(x="sports_or_wagon", y='price', data=df, order=2)
Target Encoding
지금까지 언급한 대부분의 기술은 숫자 형태의 피쳐에 대한 것입니다. 지금부터 살펴볼 기술인 대상 인코딩(Target Encoding)은 범주 형태의 피쳐를 위한 것입니다. 원-핫 또는 레이블 인코딩과 같이 범주를 숫자로 인코딩하는 방법이지만 대상을 사용하여 인코딩을 생성한다는 차이점이 있습니다. 이것은 우리가 지도적 피쳐 공학 기술(supervised feature engineering technique)이라고 부르는 것입니다.
1
2
3
import pandas as pd
autos = pd.read_csv("input_data/autos.csv", na_values='?')
대상 인코딩은 피쳐의 범주를 대상에서 파생 된 일부 숫자로 대체하는 모든 종류의 인코딩입니다.
간단하고 효과적인 방법은 Creating Features 파트에서 다뤘던 평균 같은 그룹 집계를 적용하는 것입니다. Automobiles 데이터 세트를 사용하여 각 차량의 평균 가격을 계산합니다.
1
2
3
autos["make-encoded"] = autos.groupby("make")["price"].transform("mean")
autos[["make", "price", "make-encoded"]].head(10)
1
2
3
4
5
6
7
8
9
10
11
make price make-encoded
0 alfa-romero 13495.0 15498.333333
1 alfa-romero 16500.0 15498.333333
2 alfa-romero 16500.0 15498.333333
3 audi 13950.0 17859.166667
4 audi 17450.0 17859.166667
5 audi 15250.0 17859.166667
6 audi 17710.0 17859.166667
7 audi 18920.0 17859.166667
8 audi 23875.0 17859.166667
9 audi NaN 17859.166667
이러한 종류의 대상 인코딩을 때때로 평균 인코딩(mean encoding)이라고합니다. 바이너리 타겟에 적용되며 빈 카운팅(bin counting)이라고도합니다.(다른 이름으로는 likelihood encoding, impact encoding, leave-one-out encoding이 있습니다.)
평활화(Smoothing)
그러나 이와 같은 인코딩에는 몇 가지 문제가 있습니다. 첫 번째는 알려지지 않은 카테고리(unknown categories)입니다. 대상 인코딩은 과적합의 특별한 위험을 초래합니다. 즉, 독립적인 “인코딩” 분할에 대해 학습해야합니다. 인코딩을 향후 분할에 결합하면 Pandas는 인코딩 분할에 없는 카테고리의 결측값을 채웁니다. 이러한 결측값은 어떻게든 대치해야합니다.
두 번째는 희귀한 카테고리(rare categories)입니다. 범주가 데이터 세트에서 너무 적으면 해당 그룹에서 계산된 통계가 매우 정확하지 않을 수 있습니다. Automobiles 데이터 세트에서 mercurcy make는 한 번만 발생합니다. 우리가 계산한 “평균” 가격은 그 차량 한 대의 가격일 뿐이며, 미래에 볼 수 있는 Mercuries를 그다지 대표하지 않을 수 있습니다. 희귀 카테고리를 인코딩하는 대상은 과적합 가능성을 높일 수 있습니다.
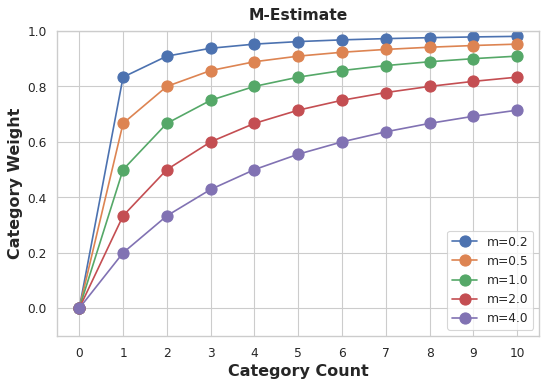
이러한 문제에 대한 해결책은 평활화(smoothing)를 추가하는 것입니다. 평활화는 카테고리 내 평균을 전체 평균과 혼합하는 것입니다. 희귀 카테고리는 카테고리 평균에 대한 가중치가 적고 누락된 카테고리는 전체 평균을 얻습니다.
1
encoding = weight * in_category + (1 - weight) * overall
여기서 weight는 카테고리 빈도에서 계산 된 0과 1 사이의 값입니다.
weight 값을 결정하는 쉬운 방법은 m-estimate를 계산하는 것입니다.
1
weight = n / (n + m)
여기서 n은 해당 범주가 데이터에서 발생하는 총 횟수입니다. 매개 변수 m은 “평활 인자(smoothing factor)”를 결정합니다. m 값이 클수록 전체 추정치에 더 많은 가중치가 부여됩니다.
Automobiles 데이터 세트의 make에는 chevrolet이 있는 3대의 자동차가 있습니다. m=2.0을 선택하면 chevrolet 카테고리는 평균 chevrolet 가격의 60%에 전체 평균 가격의 40%를 더한 값으로 인코딩됩니다.
1
chevrolet = 0.6 * 6000.00 + 0.4 * 13285.03
m에 대한 값을 선택할 때 범주가 얼마나 노이즈가 클 것으로 예상하는지 고려하십시오. 차량 가격은 각 제조사마다 매우 다양합니까? 좋은 견적을 얻으려면 많은 데이터가 필요합니까? 그렇다면 m에 대해 더 큰 값을 선택하는 것이 좋습니다. 각 제조사의 평균 가격이 비교적 안정적이라면 더 작은 값이 괜찮을 수 있습니다.
대상 인코딩의 사용 사례
- 높은 카디널리티 피쳐(High-cardinality features) 범주가 많은 피쳐는 인코딩하기가 번거로울 수 있습니다. 원-핫 인코딩은 너무 많은 피쳐를 생성하고 레이블 인코딩과 같은 대안은 해당 피쳐에 적합하지 않을 수 있습니다. 대상 인코딩은 피쳐의 가장 중요한 속성인 대상과의 관계를 사용하여 범주에 대한 숫자를 도출합니다.
- 도메인 동기 기능(Domain-motivated features) 우리는 이전 경험을 통해, 피쳐 메트릭에서 점수가 낮게 나오더라도 범주형 피쳐가 중요할지도 모른다는 의심을 할 수 있습니다. 대상 인코딩은 피쳐의 진정한 정보 가치를 드러내는 데 도움이 될 수 있습니다.
Example - MovieLens1M
MovieLens1M 데이터 세트에는 MovieLens 웹 사이트 사용자의 1백만 영화의 등급이 포함되어 있으며 각 사용자 및 영화를 설명하는 기능이 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import warnings
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
"axes",
labelweight="bold",
labelsize="large",
titleweight="bold",
titlesize=14,
titlepad=10,
)
warnings.filterwarnings('ignore')
df = pd.read_csv("input_data/movielens1m.csv")
df = df.astype(np.uint8, errors='ignore') # reduce memory footprint
print("Number of Unique Zipcodes: {}".format(df["Zipcode"].nunique()))
1
Number of Unique Zipcodes: 3439
3000개가 넘는 카테고리가 있는 Zipcode 피쳐는 대상 인코딩에 적합한 후보가 되며, 이 데이터 세트의 크기(100만 행 이상)는 인코딩을 생성하기 위해 일부 데이터를 절약 할 수 있음을 의미합니다.
대상 인코더를 학습시키기 위해 25% 분할을 생성하는 것으로 시작합니다.
1
2
3
4
5
6
7
X = df.copy()
y = X.pop('Rating')
X_encode = X.sample(frac=0.25)
y_encode = y[X_encode.index]
X_pretrain = X.drop(X_encode.index)
y_train = y[X_pretrain.index]
scikit-learn-contrib의 category_encoders 패키지는 Zipcode 기능을 인코딩하는 데 사용할 m-estimate 인코더를 구현합니다.
1
2
3
4
5
6
7
8
9
10
from category_encoders import MEstimateEncoder
# Create the encoder instance. Choose m to control noise.
encoder = MEstimateEncoder(cols=["Zipcode"], m=5.0)
# Fit the encoder on the encoding split.
encoder.fit(X_encode, y_encode)
# Encode the Zipcode column to create the final training data
X_train = encoder.transform(X_pretrain)
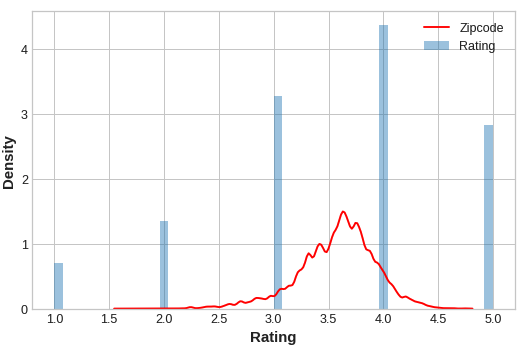
인코딩 된 값을 대상과 비교하여 인코딩이 얼마나 유익한지 살펴보겠습니다.
1
2
3
4
5
plt.figure(dpi=90)
ax = sns.distplot(y, kde=False, norm_hist=True)
ax = sns.kdeplot(X_train.Zipcode, color='r', ax=ax)
ax.set_xlabel("Rating")
ax.legend(labels=['Zipcode', 'Rating'])
인코딩 된 Zipcode 피쳐의 배포는 대략 실제 등급의 분포를 따르며, 이는 영화 감상자들이 우리의 대상 인코딩이 유용한 정보를 캡처 할 수 있을만큼 zipcode에서 zipcode까지 등급이 충분히 달랐음을 의미합니다.