Intro to Machine Learning
목차
- 모델의 작동 방식
- 기본 데이터 탐색
- 첫 번째 기계 학습 모델
- 모델 유효성 검사
- 언더피팅 및 오버피팅
- 랜덤 포레스트
모델의 작동 방식
먼저 기계 학습 모델의 작동 방식 및 사용 방법에 대한 개요부터 살펴보겠습니다. 이전에 통계 모델링이나 기계 학습을 한 적이 있는 경우 이는 기본처럼 느껴질 수 있습니다. 걱정하지 마세요, 우리는 곧 강력한 모델을 만들 거예요.
이 마이크로코스는 다음과 같은 시나리오를 진행할 때 모델을 제작합니다.
여러분의 사촌은 부동산 투기를 하면서 수백만 달러를 벌었습니다. 여러분이 데이터 과학에 관심을 가졌던 덕분에 그는 여러분과 비즈니스 파트너가 되겠다고 제안했습니다. 그는 돈을 공급할 것이고, 여러분은 다양한 집들의 가치를 예측하는 모델을 제공할 것입니다.
여러분은 사촌에게 과거에 부동산 가치를 어떻게 예측했는지를 물어봤더니 그는 그저 직감으로 했다고 합니다. 하지만 더 많은 의문점을 들춰보면, 그는 과거에 보았던 주택에서 가격 패턴을 알아냈고, 그가 고려하고 있는 새로운 주택에 대한 예측을 하기 위해 그 패턴을 사용한다는 것입니다.
기계 학습도 같은 방식으로 작동합니다. 먼저 의사 결정 트리(Decision Tree)라는 모델로 시작하겠습니다. 물론 더 정확한 예측을 해주는 더 멋진 모델들이 존재하지만, 의사 결정 트리는 이해하기 쉽고 데이터 과학에서 가장 우수한 일부 모델의 기본 구성 요소입니다.
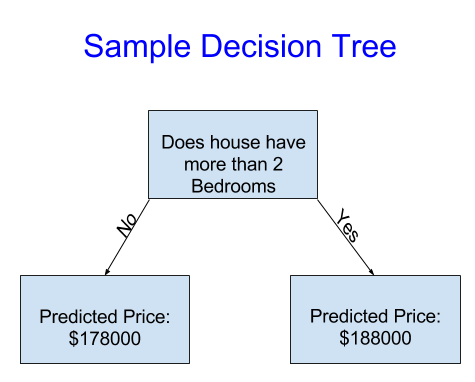
단순성을 위해 가장 간단한 의사 결정 트리부터 살펴보겠습니다.
그것은 집을 단지 두 개의 범주로 나눕니다. 고려 대상 주택의 예상가격은 동일한 범주에 속하는 주택의 역사적 평균가격입니다.
우리는 데이터를 사용하여 집을 두 그룹으로 나누는 방법을 결정하고, 다시 각 그룹의 예상 가격을 결정합니다. 데이터에서 패턴을 포착하는 이 단계를 모델 적합(fitting) 또는 훈련(training)이라고 합니다. 모형을 적합시키는 데 사용되는 데이터를 training data라고 합니다.
모델이 얼마나 적합한지에 대한 세부 내용(예: 데이터를 분할하는 방법)은 복잡하지만 나중에 저장할 수 있습니다. 모델이 적합된 후에는 이를 새 데이터에 적용하여 추가된 주택의 가격을 예측할 수 있습니다.
의사 결정 트리 개선
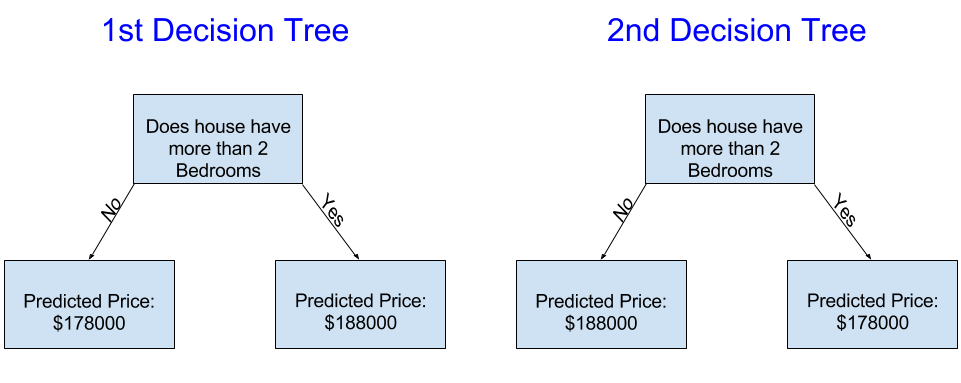
다음 두 가지 의사 결정 트리 중 부동산 교육 데이터를 적합(fitting)하여 얻을 가능성이 더 높은 것은 무엇입니까?
왼쪽의 의사 결정 트리(1st Decision Tree)는 침실이 더 많은 주택이 침실이 적은 주택보다 높은 가격에 판매되는 경향이 있다는 현실을 포착하기 때문에 더 의미가 있을 수 있습니다. 이 모델의 가장 큰 단점은 화장실 수, lot size(집과 마당을 모두 포함시킨 크기), 위치 등 집값에 영향을 미치는 대부분의 요인을 포착하지 못한다는 것입니다.
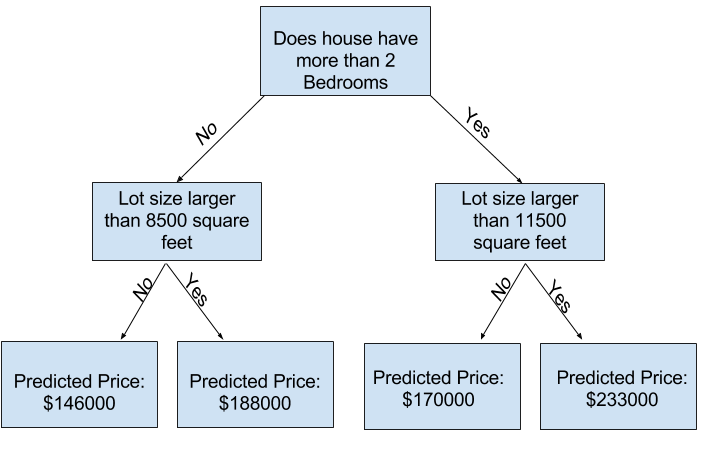
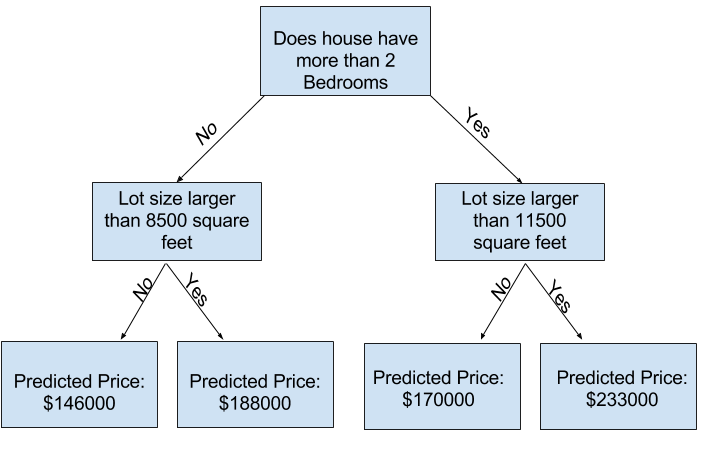
여러분은 더 많은 “분할(splits)”이 있는 트리를 사용하여 더 많은 요인을 수용할 수 있습니다. 이것들은 “더 깊은(deeper)” 트리라고 불립니다. 각 집 부지의 총 크기를 고려하는 의사 결정 트리는 다음과 같을 수 있습니다.
의사 결정 트리를 추적하여 항상 해당 주택의 특성에 해당하는 경로를 선택하여 주택 가격을 예측합니다. 집의 예상 가격은 트리의 밑바닥에 있습니다. 우리가 예측하는 바닥의 지점을 리프(leaf)라고합니다.
리프들의 분할과 값은 데이터에 의해 결정되므로 작업 할 데이터를 확인해야합니다.
기본 데이터 탐색
Pandas
- pandas docs
- pandas 라이브러리 설치
1
2
3
```shell
conda install pandas
```
머신 러닝 프로젝트의 첫 번째 단계는 데이터에 익숙해지는 것입니다. pandas 라이브러리를 이용해봅시다. pandas는 과학자들이 데이터를 탐색하고 조작하는 데 사용하는 주요 도구 데이터입니다. 대부분의 사람들은 아래와 같이 pandas를 축약형으로 pd라고 씁니다.
1
import pandas as pd
pandas 라이브러리의 가장 중요한 부분은 데이터 프레임(DataFrame)입니다. 데이터 프레임은 여러분이 테이블이라 생각할 수 있는 데이터 유형을 저장합니다. 이것은 Excel의 시트 또는 SQL 데이터베이스의 테이블과 유사합니다.
pandas는 이런 종류의 데이터로 여러분이 하고 싶어하는 대부분의 것들에 대한 강력한 방법을 가지고 있습니다.
예를 들어, 호주 멜버른의 집값에 대한 데이터를 살펴보겠습니다. 실습에서는 동일한 프로세스를 아이오와에 있는 집값이 포함된 새 dataset에 적용합니다.
다음 코드를 사용하여 데이터를 로드하고 탐색할 수 있습니다.
1
2
3
4
5
6
# save filepath to variable for easier access
melbourne_file_path = 'input_data/melb_data.csv'
# read the data and store data in DataFrame titled melbourne_data
melbourne_data = pd.read_csv(melbourne_file_path)
# print a summary of the data in Melbourne data
melbourne_data.describe()
1
2
3
4
5
6
7
8
9
10
11
Unnamed: 0 Rooms ... Longtitude Propertycount
count 18396.000000 18396.000000 ... 15064.000000 18395.000000
mean 11826.787073 2.935040 ... 144.996338 7517.975265
std 6800.710448 0.958202 ... 0.106375 4488.416599
min 1.000000 1.000000 ... 144.431810 249.000000
25% 5936.750000 2.000000 ... 144.931193 4294.000000
50% 11820.500000 3.000000 ... 145.000920 6567.000000
75% 17734.250000 3.000000 ... 145.060000 10331.000000
max 23546.000000 12.000000 ... 145.526350 21650.000000
[8 rows x 14 columns]
데이터 설명 해석
결과는 원본 데이터 집합의 각 열에 대해 8개의 숫자를 표시합니다. 첫 번째 숫자, 카운트는 비결측값(non-missing values)을 가진 행 수를 나타냅니다.
결측값은 여러 가지 이유로 인해 발생합니다. 예를 들어, 침실 1채의 집을 조사할 때 침실 2개의 크기는 수집되지 않습니다. 데이터 누락에 대한 주제로 돌아가겠습니다.
두 번째 값은 mean, 즉 평균입니다. 여기서 std는 표준 편차이며, 이 값은 숫자적으로 얼마나 퍼져 있는지 측정합니다.
min, 25%, 50%, 75%, max를 해석하려면 각 열을 가장 낮은 값에서 가장 높은 값으로 정렬한다고 가정해 보십시오. 첫 번째(가장 작은) 값은 min입니다. 이 목록에서 25%, 75%보다 작은 숫자를 찾을 수 있습니다. 이는 25% 값(“25번째 백분위수”)입니다. 50번째 백분위수와 75번째 백분위수가 유사하게 정의되며 max는 가장 큰 숫자입니다.
첫 번째 기계 학습 모델
모델링을 위한 데이터 선택
dataset에는 너무 많은 변수가 있어서 여러분이 이해하거나 출력하기가 어렵습니다. 어떻게 하면 이 엄청난 양의 데이터를 이해할 수 있도록 나눌 수 있을까요?
먼저 여러분의 직관을 이용해 몇 가지 변수를 고르는 것으로 시작하겠습니다. 이후 과정에서는 변수의 우선 순위를 자동으로 정하는 통계 기법을 보여줄겁니다.
variables/columns를 선택하려면 데이터 집합의 모든 columns 목록을 확인해야 합니다. 이 작업은 DataFrame의 columns property로 수행됩니다.
1
2
3
4
5
import pandas as pd
melbourne_file_path = 'input_data/melb_data.csv'
melbourne_data = pd.read_csv(melbourne_file_path)
melbourne_data.columns
1
2
3
4
5
Index(['Unnamed: 0', 'Suburb', 'Address', 'Rooms', 'Type', 'Price', 'Method',
'SellerG', 'Date', 'Distance', 'Postcode', 'Bedroom2', 'Bathroom',
'Car', 'Landsize', 'BuildingArea', 'YearBuilt', 'CouncilArea',
'Lattitude', 'Longtitude', 'Regionname', 'Propertycount'],
dtype='object')
1
2
3
4
5
6
7
8
# The Melbourne data has some missing values (some houses for which some variables weren't recorded.)
# We'll learn to handle missing values in a later tutorial.
# Your Iowa data doesn't have missing values in the columns you use.
# So we will take the simplest option for now, and drop houses from our data.
# Don't worry about this much for now, though the code is:
# dropna drops missing values (think of na as "not available")
melbourne_data = melbourne_data.dropna(axis=0)
데이터의 하위 집합을 선택하는 방법은 여러 가지가 있습니다. Pandas Micro-Course에서는 이러한 것들을 더 심도 있게 다루지만, 우리는 현재로선 두 가지 접근법에 초점을 맞출 것입니다.
- 점 표기법(Dot notation), “예측 대상(prediction target)”을 선택하는 데 사용됩니다.
- 열 목록으로 선택(Selecting with a column list), “피쳐(features)”을 선택하는 데 사용됩니다.
예측 대상(prediction target) 선택
점 표기법(Dot notation)으로 변수를 추출 할 수 있습니다. 이 단일 열(single column)은 단일 데이터 열만있는 DataFrame과 대체로 유사한 Series에 저장됩니다.
점 표기법을 사용하여 예측할 열을 선택합니다. 이를 예측 대상(prediction target)이라고합니다. 관례 적으로 예측 대상을 y라고합니다.
1
y = melbourne_data.Price
피쳐(features) 선택
모델에 입력되고 나중에 예측에 사용되는 열을 “피쳐(features)”라고합니다. 우리의 경우 주택 가격을 결정하는 데 사용되는 열이 될 것입니다. 때로는 대상을 제외한 모든 열을 피쳐로 사용합니다. 다른 경우에는 여러분은 더 적은 피쳐로 더 나아질 수 있습니다.
지금은 몇 가지 피쳐만 포함 된 모델을 작성하겠습니다. 나중에 다른 피쳐로 빌드 된 모델을 반복하고 비교하는 방법을 볼 수 있습니다.
대괄호 안에 열 이름 목록을 제공하여 여러 피쳐를 선택합니다. 해당 목록의 각 항목은 따옴표로 구분된 문자열이어야합니다.
여기 예제문이 있습니다.
1
melbourne_features = ['Rooms', 'Bathroom', 'Landsize', 'Lattitude', 'Longtitude']
관례적으로, 이 데이터를 X라고 합니다.
1
X = melbourne_data[melbourne_features]
describe 메서드와 맨 위 몇 행을 표시하는 head 메서드를 사용하여 주택 가격을 예측하는 데 사용할 데이터를 빠르게 검토해 보겠습니다.
1
X.describe()
1
2
3
4
5
6
7
8
9
Rooms Bathroom Landsize Lattitude Longtitude
count 6196.000000 6196.000000 6196.000000 6196.000000 6196.000000
mean 2.931407 1.576340 471.006940 -37.807904 144.990201
std 0.971079 0.711362 897.449881 0.075850 0.099165
min 1.000000 1.000000 0.000000 -38.164920 144.542370
25% 2.000000 1.000000 152.000000 -37.855438 144.926198
50% 3.000000 1.000000 373.000000 -37.802250 144.995800
75% 4.000000 2.000000 628.000000 -37.758200 145.052700
max 8.000000 8.000000 37000.000000 -37.457090 145.526350
1
X.head()
1
2
3
4
5
6
Rooms Bathroom Landsize Lattitude Longtitude
1 2 1.0 156.0 -37.8079 144.9934
2 3 2.0 134.0 -37.8093 144.9944
4 4 1.0 120.0 -37.8072 144.9941
6 3 2.0 245.0 -37.8024 144.9993
7 2 1.0 256.0 -37.8060 144.9954
이러한 명령으로 데이터를 시각적으로 확인하는 것은 data scientist의 업무에서 중요한 부분입니다. 여러분은 추가 검사가 필요한 dataset에서 놀라움을 자주 찾을 수 있습니다.
모델 구축
scikit-learn 라이브러리를 사용하여 모델을 만듭니다. 코딩 할 때 이 라이브러리는 샘플 코드에서 볼 수 있듯이 sklearn으로 작성됩니다. Scikit-learn은 일반적으로 DataFrames에 저장된 데이터 유형을 모델링하는 데 가장 널리 사용되는 라이브러리입니다.
- 사이킷런 라이브러리 설치하기
1
2
3
```shell
pip install scikit-learn
```
모델을 구축하고 사용하는 단계는 다음과 같습니다.
- 정의(Define) 어떤 유형의 모델이 될지? 의사 결정 트리? 다른 유형의 모델? 모델 유형의 다른 매개 변수도 지정됩니다.
- 적합(Fit) 제공된 데이터에서 패턴을 캡처(capture)합니다. 이것이 모델링의 핵심입니다.
- 예측(Predict) 말 그대로
- 평가(Evaluate) 모델의 예측이 얼마나 정확한지 확인합니다.
다음은 scikit-learn으로 의사 결정 트리 모델을 정의하고 피쳐(features) 및 대상 변수(target variable)에 fitting하는 예시입니다.
1
2
3
4
5
6
7
from sklearn.tree import DecisionTreeRegressor
# Define model. Specify a number for random_state to ensure same results each run
melbourne_model = DecisionTreeRegressor(random_state=1)
# Fit model
melbourne_model.fit(X, y)
1
DecisionTreeRegressor(random_state=1)
많은 기계 학습 모델은 모델 학습에서 약간의 임의성을 허용합니다. random_state에 숫자를 지정하면 각 실행에서 동일한 결과를 얻을 수 있습니다. 이것은 좋은 관행으로 간주됩니다. 어떤 숫자를 사용하든 모델 품질은 선택한 값에 따라 크게 달라지지 않습니다.
이제 여러분에겐 예측에 사용할 수 있는 fitted model이 생겼습니다.
실제로, 우리가 이미 가격을 책정 한 주택보다는 시장에 출시 될 새 주택에 대한 예측을 하고 싶을 것입니다. 그러나 먼저, 예측 기능이 어떻게 작동하는지 알아보기 위해 훈련 데이터의 처음 몇 행에 대한 예측을 수행해봅시다.
1
2
3
4
print("Making predictions for the following 5 houses:")
print(X.head())
print("The predictions are")
print(melbourne_model.predict(X.head()))
1
2
3
4
5
6
7
8
9
Making predictions for the following 5 houses:
Rooms Bathroom Landsize Lattitude Longtitude
1 2 1.0 156.0 -37.8079 144.9934
2 3 2.0 134.0 -37.8093 144.9944
4 4 1.0 120.0 -37.8072 144.9941
6 3 2.0 245.0 -37.8024 144.9993
7 2 1.0 256.0 -37.8060 144.9954
The predictions are
[1035000. 1465000. 1600000. 1876000. 1636000.]
모델 검증
모델을 만들었습니다. 하지만 얼마나 좋은 모델일까요?
이 단원에서는 모델 유효성 검사를 사용하여 모델의 품질을 측정하는 방법을 배웁니다. 모델 품질 측정은 모델을 반복적으로 개선하기 위한 핵심입니다.
모델 검증이란?
여러분은 지금까지 구축 한 거의 모든 모델을 평가하고 싶을 것입니다. 전부는 아니지만 대부분의 애플리케이션에서 모델 품질의 관련 척도는 예측 정확도(predictive accuracy)입니다. 즉, 모델의 예측이 실제로 발생하는 것과 비슷할 것입니다.
많은 사람들이 예측 정확도를 측정 할 때 큰 실수를 합니다. 학습 데이터로 예측을 수행하고 이러한 예측을 학습 데이터의 목표 값과 비교합니다. 이 접근 방식의 문제와 해결 방법을 곧 알게 될 것이지만, 먼저 어떻게해야할지 생각해 보겠습니다.
먼저 모델 품질을 이해할 수 있는 방식으로 요약해야합니다. 10,000 개의 주택에 대한 예상 주택 값과 실제 주택 값을 비교하면 좋은 예측과 나쁜 예측이 혼합 된 것을 찾을 수 있습니다. 10,000 개의 예측 및 실제 값 목록을 살펴 보는 것은 무의미합니다. 이것을 하나의 지표로 요약해야합니다.
모델 품질을 요약하는 데는 여러 가지 메트릭이 있지만 MAE라고도하는 평균 절대 오차(Mean Absolute Error)라는 메트릭부터 시작하겠습니다. 마지막 단어인 error로 시작하여 이 측정 항목을 분석해 보겠습니다.
각 주택의 예측 오차는 다음과 같습니다.
1
error = actual − predicted
따라서 실제 집값이 $150,000이고 $100,000라고 예측했다면 error는 $50,000입니다.
이제 MAE 메트릭을 사용하여 각 오류에 절대값을 취합니다. 이렇게하면 각 오류가 양수로 변환됩니다. 그런 다음 이렇게 구한 오류의 절대값들에 대한 평균을 구합니다. 이것이 우리의 모델 품질의 측정입니다. 평문으로는 다음과 같이 말할 수 있습니다.
1
2
On average, our predictions are off by about X.
평균적으로 우리의 예측은 약 X만큼 떨어져 있습니다.
MAE를 계산하려면 먼저 모델이 필요합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
# Load data
melbourne_file_path = 'input_data/melb_data.csv'
melbourne_data = pd.read_csv(melbourne_file_path)
# Filter rows with missing price values
filtered_melbourne_data = melbourne_data.dropna(axis=0)
# Choose target and features
y = filtered_melbourne_data.Price
melbourne_features = [
'Rooms', 'Bathroom', 'Landsize', 'BuildingArea', 'YearBuilt',
'Lattitude', 'Longtitude'
]
X = filtered_melbourne_data[melbourne_features]
# Define model
melbourne_model = DecisionTreeRegressor()
# Fit model
melbourne_model.fit(X, y)
모델이 생성되면 평균 절대 오차를 계산하는 방법은 다음과 같습니다.
1
2
3
4
from sklearn.metrics import mean_absolute_error
predicted_home_prices = melbourne_model.predict(X)
mean_absolute_error(y, predicted_home_prices)
1
434.71594577146544
“표본 내 데이터(In-Sample)” 점수(Scores)의 문제
방금 계산 한 측정 값을 “표본 내 데이터(In-Sample)” 점수(Scores)라고 할 수 있습니다. 우리는 모델을 구축하고 평가하기 위해 단일 “sample” 주택을 사용했습니다. 이것이 나쁜 이유입니다.
대형 부동산 시장에서 문 색상이 주택 가격과 무관하다고 상상해보십시오.
그러나 모델을 구축하는 데 사용한 데이터 샘플에서 녹색 문이 있는 모든 집은 매우 비쌌습니다. 모델의 역할은 주택 가격을 예측하는 패턴을 찾는 것이므로이 패턴을 보고 녹색 문이 있는 주택의 가격을 항상 높게 예측합니다.
모델의 실질적인 가치는 새로운 데이터에 대한 예측에서 비롯되므로 모델을 구축하는 데 사용되지 않은 데이터의 성능을 측정합니다. 이를 수행하는 가장 간단한 방법은 모델 구축 프로세스에서 일부 데이터를 제외하고 이를 사용하여 이전에 보지 못한 데이터에 대한 모델의 정확성을 테스트하는 것입니다. 이 데이터를 유효성 검사 데이터(validation data)라고합니다.
코딩
scikit-learn 라이브러리에는 데이터를 두 조각으로 나누는 train_test_split 함수가 있습니다. 이 데이터 중 일부를 모델에 맞는 학습 데이터로 사용하고 다른 데이터를 유효성 검사 데이터로 사용하여 mean_absolute_error를 계산합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import pandas as pd
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split
# Load data
melbourne_file_path = 'input_data/melb_data.csv'
melbourne_data = pd.read_csv(melbourne_file_path)
# Filter rows with missing price values
filtered_melbourne_data = melbourne_data.dropna(axis=0)
# Choose target and features
y = filtered_melbourne_data.Price
melbourne_features = [
'Rooms', 'Bathroom', 'Landsize', 'BuildingArea', 'YearBuilt',
'Lattitude', 'Longtitude'
]
X = filtered_melbourne_data[melbourne_features]
# split data into training and validation data, for both features and target
# The split is based on a random number generator. Supplying a numeric value to
# the random_state argument guarantees we get the same split every time we
# run this script.
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=0)
# Define model
melbourne_model = DecisionTreeRegressor()
# Fit model
melbourne_model.fit(train_X, train_y)
# get predicted prices on validation data
val_predictions = melbourne_model.predict(val_X)
print(mean_absolute_error(val_y, val_predictions))
1
259904.41510652035
표본 내 데이터(In-Sample)의 평균 절대 오차는 약 450 달러였습니다. 표본 외 데이터(Out-of-sample)는 250,000 달러 이상입니다.
이것은 거의 정확히 맞는 모델과 가장 실용적인 목적으로 사용할 수 없는 모델의 차이점입니다. 참고로, 검증 데이터의 평균 주택 가치는 110 만 달러입니다. 따라서 새 데이터의 오류는 평균 주택 가치의 약 1/4입니다.
더 나은 기능이나 다른 모델 유형을 찾기 위한 실험과 같이 이 모델을 개선하는 방법에는 여러 가지가 있습니다.
Underfitting & Overfitting
이 단계가 끝나면 과소적합(underfitting) 및 과적합(overfitting)의 개념을 이해하고 이러한 아이디어를 적용하여 모델을 더 정확하게 만들 수 있습니다.
다른 모델로 실험
이제 모델 정확도 측정이 가능한 신뢰할 수 있는 방법이 있으므로 대체 모델(alternative models)을 실험하고 어떤 것이 가장 좋은 예측을 제공하는지 확인할 수 있습니다. 그럼 모델에 대해 어떤 대안이 있습니까?
scikit-learn의 문서에서 의사 결정 트리 모델에 많은 옵션이 있음을 알 수 있습니다. 가장 중요한 옵션은 트리의 깊이를 결정합니다. 이 micro-course의 첫 번째 강의에서 트리의 깊이는 예측을 하기 전에 얼마나 많은 분할을 하는지에 대한 척도라는 것을 상기하십시오. 이것은 비교적 얕은 트리입니다.
실제로 트리가 최상위 레벨(모든 집)과 리프(leaf) 사이에 10 개의 분할을 갖는 것은 드문 일이 아닙니다. 트리가 깊어짐에 따라 dataset는 더 적은 수의 집이 있는 리프(leaf)로 나뉩니다. 트리에 1 개의 분할 만있는 경우 데이터를 2 개의 그룹으로 나눕니다. 각 그룹이 다시 분할되면 우리는 4 그룹의 집을 얻습니다. 각각을 다시 분할하면 8 개의 그룹이 생성됩니다. 각 레벨에서 더 많은 분할을 추가하여 그룹 수를 계속 두 배로 늘리면 10 레벨에 도달 할 때까지 210 개의 주택 그룹이 생깁니다. 1024 개의 리프(leaf)입니다.
여러 리프(leaf) 사이에서 집을 나눌 때 우리는 또한 각 리프(leaf)에 집이 적습니다. 집이 거의없는 나뭇잎은 해당 집의 실제 값에 매우 가까운 예측을 할 수 있지만 새 데이터에 대해 매우 신뢰할 수 없는 예측을 할 수도 있습니다(각 예측은 몇 집만 기반으로하기 때문).
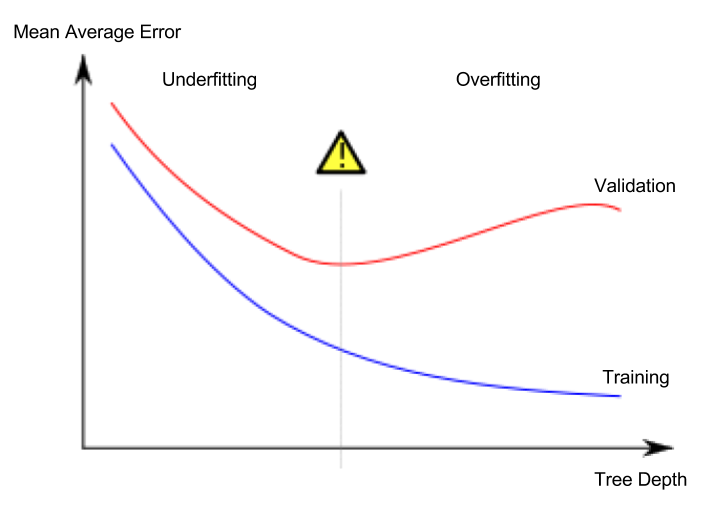
이것은 모델이 훈련 데이터와 거의 완벽하게 일치하지만 유효성 검사 및 기타 새 데이터에서는 제대로 작동하지 않는 과적합(overfitting)이라고 하는 현상입니다. 반대로 우리가 트리를 매우 얕게 만들면 집의 그룹을 너무 적게 만들 수도 있습니다.
극단적으로 트리가 집을 2 개 또는 4 개로만 나누더라도 각 그룹에는 여전히 다양한 집이 있습니다. 결과 예측은 훈련 데이터에서도 대부분의 주택에서 멀리 떨어져있을 수 있습니다(동일한 이유로 유효성 검사에서도 좋지 않습니다). 모델이 데이터에서 중요한 구별과 패턴을 캡처하지 못하여 학습 데이터에서도 성능이 저하되는 경우, 이를 과소적합(underfitting)이라고합니다.
검증 데이터에서 추정 한 새 데이터의 정확성에 관심이 있으므로 과소적합과 과적합 사이의 최적 지점을 찾고 싶습니다. 시각적으로 우리는 (빨간색) 검증 곡선의 낮은 지점을 원합니다.
예시
트리 깊이를 제어하기 위한 몇 가지 대안이 있으며 많은 경우 트리를 통과하는 일부 경로가 다른 경로보다 더 큰 깊이를 가질 수 있습니다. 그러나 max_leaf_nodes 인수는 과적 합과 과소 적합을 제어하는 매우 합리적인 방법을 제공합니다. 모델이 만들 수있는 잎이 많을수록 위 그래프의 적합하지 않은 영역에서 과적 합 영역으로 더 많이 이동합니다.
함수를 정의하여 max_leaf_nodes에 대한 다른 값의 MAE 점수를 비교할 수 있습니다.
1
2
3
4
5
6
7
8
9
from sklearn.metrics import mean_absolute_error
from sklearn.tree import DecisionTreeRegressor
def get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y):
model = DecisionTreeRegressor(max_leaf_nodes=max_leaf_nodes, random_state=0)
model.fit(train_X, train_y)
preds_val = model.predict(val_X)
mae = mean_absolute_error(val_y, preds_val)
return mae
우리는 이제 for 루프를 사용하여 max_leaf_nodes에 대해 서로 다른 값으로 빌드 된 모델의 정확도를 비교할 수 있습니다.
1
2
3
4
# compare MAE with differing values of max_leaf_nodes
for max_leaf_nodes in [5, 50, 500, 5000]:
my_mae = get_mae(max_leaf_nodes, train_X, val_X, train_y, val_y)
print("Max leaf nodes: %d \t\t Mean Absolute Error: %d" %(max_leaf_nodes, my_mae))
1
2
3
4
Max leaf nodes: 5 Mean Absolute Error: 347380
Max leaf nodes: 50 Mean Absolute Error: 258171
Max leaf nodes: 500 Mean Absolute Error: 243495
Max leaf nodes: 5000 Mean Absolute Error: 254983
나열된 옵션 중 500이 최적의 리프(leaf) 수 입니다.
결론
요점은 다음과 같습니다.
- 과적합 미래에 재발하지 않고 덜 정확한 예측으로 이어지는 가짜 패턴을 캡처합니다.
- 과소적합 관련 패턴을 포착하지 못해 예측 정확도가 떨어집니다.
모델 학습에 사용되지 않는 검증 데이터를 사용하여 후보 모델의 정확도를 측정합니다. 이를 통해 많은 후보 모델을 시도하고 최상의 모델을 유지할 수 있습니다.
랜덤 포레스트(Random Forests)
의사 결정 트리는 어려운 결정을 내립니다. 리프(leaf)가 많은 깊은 트리는 각 예측이 리프(leaf)에 있는 몇 집의 과거 데이터에서 나오기 때문에 과적합됩니다. 그러나 리프(leaf) 거의 없는 얕은 트리는 원시 데이터에서 많은 구별을 캡처하지 못하므로 성능이 저하됩니다.
오늘날 가장 정교한 모델링 기술조차도 과적합(overfitting)과 과소적합(underfitting) 사이의 긴장에 직면 해 있습니다. 그러나 많은 모델이 더 나은 성능으로 이어질 수있는 영리한 아이디어를 가지고 있습니다. 랜덤 포레스트(Random Forests)를 예로 들어 보겠습니다.
랜덤 포레스트(Random Forests)는 많은 트리를 사용하며 각 구성 요소 트리의 예측을 평균하여 예측합니다. 일반적으로 단일 의사 결정 트리보다 예측 정확도가 훨씬 뛰어나며 기본 매개 변수와 잘 작동합니다. 모델링을 계속하면 더 나은 성능으로 더 많은 모델을 배울 수 있지만 많은 모델이 올바른 매개 변수를 얻는 데 민감합니다.
예시
우리는 위에서 데이터를 로드하는 코드를 이미 몇 번 보았습니다. 데이터 로딩이 끝나면 다음과 같은 변수가 있습니다.
- train_X
- val_X
- train_y
- val_y
우리는 scikit-learn에서 의사 결정 트리를 구축 한 방법과 유사하게 랜덤 포레스트 모델을 구축합니다. 이번에는 DecisionTreeRegressor 대신 RandomForestRegressor 클래스를 사용합니다.
1
2
3
4
5
6
7
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
forest_model = RandomForestRegressor(random_state=1)
forest_model.fit(train_X, train_y)
melb_preds = forest_model.predict(val_X)
print(mean_absolute_error(val_y, melb_preds))
1
191669.7536453626
결론
추가 개선의 여지가있을 수 있지만 이는 최상의 의사 결정 트리 오류였던 250,000보다 큰 개선입니다. 단일 의사 결정 트리의 최대 깊이를 변경 한 것처럼 Random Forest의 성능을 변경할 수 있는 매개 변수가 있습니다. 그러나 Random Forest 모델의 가장 큰 특징 중 하나는 이러한 조정 없이도 일반적으로 합리적으로 작동한다는 것입니다.